In the picture of Fig. 6.10, you see in action a fundamental force of nature (called the Lorentz force) acting on particles with electric charge \(q\). The Lorentz force is expressed by the relation \(\mathbf{F}=q \mathbf{v} \times \mathbf{B}\) where \(\mathbf{v}\) is the velocity of the particle, and \(\mathbf{B}\) a vector called the magnetic field. The units of \(q\) and \(B\) in the International System are Coulomb (C) and Tesla (T), so that the force is in Newtons if the velocity is expressed in \(\mathrm{m} / \mathrm{s}\). At point \(\mathrm{O}\) in the picture, a device emits electrons (particles of mass \(m=9.11 \times 10^{-31} \mathrm{~kg}\) and negative charge \(q=-1.60 \times 10^{-19} \mathrm{C}\) ) with initial velocity \(v_{0} \hat{\mathbf{i}}\) in a region with uniform \(\mathbf{B}\) and directed perpendicularly to the figure plane, \(\mathbf{B}=B_{0} \hat{\mathbf{k}}\) and \(B_{0}=4.60 \times 10^{-4} \mathrm{~T}\). As a result of the action of the Lorentz force, the observed trajectory (practically circular) has radius \(R=3.25 \mathrm{~cm}\). Determine from the given data

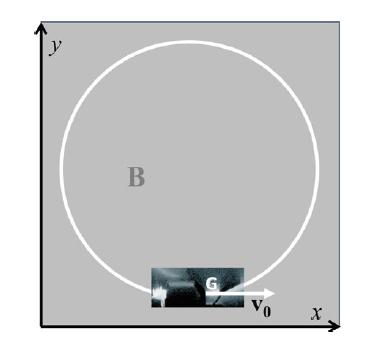
1. The force, acting on an electron at the point \(\mathrm{O}\) in the figure (draw the direction) and the speed \(v_{0}\) with which the electrons are input, in terms of the speed of light \(=3.00 \times 10^{8} \mathrm{~m} / \mathrm{s}\).
2. The time taken by an electron to travel around the circumference.
3. The work done by the Lorentz force on an electron from point \(\mathrm{O}\) to \(\mathrm{A}\) (point A placed at 5/12 of the length of the circumference).
4. The speed with which the electron arrives at point A.
5. The vector \(\mathbf{B}\) is entering or exiting from the sheet?

Transcribed Image Text:

y B G X