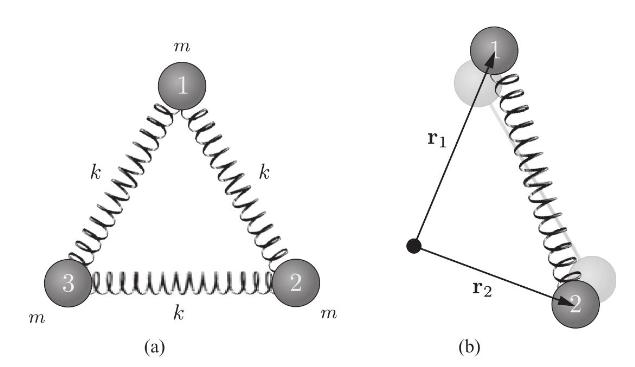
In the previous problem, three degenerate normal modes were derived for the case of three equal masses at the vertices of an equilateral triangle, where the springs form the sides of the triangle. Any other oscillation in which the CM remains at rest and the system has no angular momentum must be a linear combination of these three modes. In particular, consider an oscillation identical to that of the second normal mode of the previous problem, except that it has been rotated to the right by \(120^{\circ}\), so for example mass No. 2 at the lower right now oscillates directly toward and away from the CM, rather than mass No. 1. By symmetry with the second normal mode, this mode should be possible, and should have the same frequency. Find the linear combination of the normal modes of the previous problem which is equal to the oscillation described above.

Data from previous problem

The techniques used can be extended to two- and three dimensional systems. For example, we can find the normal-mode oscillations of a system of three equal masses \(m\) and three equal springs \(k\) in the configuration of an equilateral triangle, as shown in Figure 13.13(a).

Transcribed Image Text:

m 3 (a) k 2 m eulu 12 (b)