The roller in the Fig. 12.1 6 consists of two mutually integral (i.e., welded) disks of the
Question:
The roller in the Fig. 12.16 consists of two mutually integral (i.e., welded) disks of the same material and density. The roller can rotate without friction around a fixed pivot coincident with the axis, arranged horizontally. Two bodies \(m_{1}=1.00 \mathrm{~kg}\) and \(m_{2}\) hang from wires (inextensible and of negligible mass) wound in opposite directions respectively on a disk of radius \(r_{1}=20.0 \mathrm{~cm}\) and on a smaller disk of radius \(r_{2}=10.0 \mathrm{~cm}\), the latter of mass \(M_{2}=589 \mathrm{~g}\). At the initial time, the system is left free to set itself in motion. It is also known that the mass \(m_{2}\) is such that, during motion, the tension \(T\) acting on the two wires are equal. It is asked to calculate:
1. The moment of inertia of the roller composed of the two overlapping disks with respect to the central pivot;
2. the angular acceleration with which the roller rotates;
3. the accelerations, \(a_{1}\) and \(a_{2}\), of the two bodies (specify which of the two bodies drops);
4. the tension \(T\) of the wires and the value of the unknown mass \(m_{2}\).
Fig. 12.16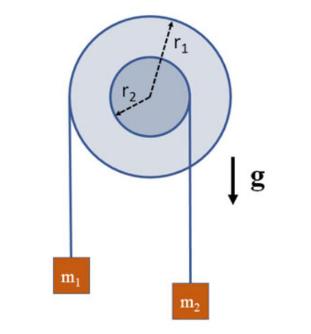
Step by Step Answer:






