A square matrix has the same number of rows and columns. Given a square matrix A, suppose
Question:
A square matrix has the same number of rows and columns. Given a square matrix A, suppose there exists a matrix B whereby AB equals a matrix in which each diagonal entry equals 1, and all other entries equal 0. You can then say that B is the inverse of A. The Excel array function MINVERSE finds the inverse of a square matrix. Use the MINVERSE function to find the inverse for matrix B in Problem 7.
Data from in Problem 7
An m-by-n matrix is a rectangular array of numbers containing m rows and n columns. The following, for example, is a 3-by-3 matrix:
Consider two matrices, A and B. Suppose that the number of columns in matrix A equals the number of rows in matrix B. Then, multiply matrix A by matrix B. (The product is written as AB.) The entry in row I and column J of AB is computed by applying the SUMPRODUCT function to row I of A and column J of B. AB will have as many rows as A and as many columns as B. The Excel MMULT function is an array function with which you can multiply matrices. Use the MMULT function to multiply the following matrices: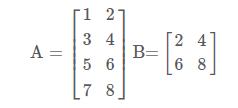
Step by Step Answer:

Microsoft Excel Data Analysis And Business Modeling
ISBN: 9780137613663
7th Edition
Authors: Wayne Winston





