(a) Consider the Penrose process, described in the text, in which a particle flying inward toward a spinning hole’s horizon splits in two inside the ergosphere, and one piece plunges into the hole while the other flies back out. Show that it is always possible to arrange this process so the plunging particle has negative energy at infinity:

(b) Around a spinning black hole consider the vector field

where Ω_H is the horizon’s angular velocity. Show that at the horizon (at radius r = r_H) this vector field is null and is tangent to the horizon generators. Show that all other vectors in the horizon are spacelike.

(c) In the Penrose process the plunging particle changes the hole’s mass by an amount △M and its spin angular momentum by an amount △J_H. Show that

Here

are to be evaluated at the event where the particle plunges through the horizon, so they both reside in the same tangent space.

(d) Show that if A(vector) is any future-directed time like vector and K(vector) is any null vector, both living in the tangent space at the same event in spacetime, then A(vector) · K(vector)

is positive, whatever may be the world line and rest mass of the plunging particle.

(e) Show that for the plunging particle to decrease the hole’s mass, it must also decrease the hole’s angular momentum (i.e., it must spin the hole down a bit).

(f) Hawking’s second law of black-hole mechanics says that, whatever may be the particle’s world line and rest mass, when the particle plunges through the horizon, it causes the horizon’s surface area A_H to increase. This suggests that the always positive quantity

might be a multiple of the increase △A_H of the horizon area. Show that this is indeed the case:

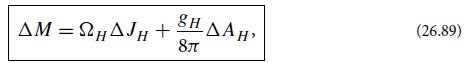
where g_H is given in terms of the hole’s mass M and the radius r_H of its horizon by

The quantity g_H is called the hole’s “surface gravity” for a variety of reasons. One reason is that an observer who hovers just above a horizon generator, blasting his or her rocket engines to avoid falling into the hole, has a 4-acceleration with magnitude g_H/α and thus feels a “gravitational acceleration” of this magnitude; here α = g^tt is a component of the Kerr metric called the lapse function [Eqs. (26.70) and (26.72)]. This gravitational acceleration is arbitrarily large for an observer arbitrarily close to the horizon (where △ and hence α are arbitrarily close to zero); when renormalized by α to make it finite, the acceleration is g_H. Equation (26.89) is called the “first law of black-hole mechanics” because of its resemblance to the first law of thermodynamics.

(g) Stephen Hawking has shown, using quantum field theory, that a black hole’s horizon emits thermal (blackbody) radiation. The temperature of this “Hawking radiation,” as measured by the observer who hovers just above the horizon, is proportional to the gravitational acceleration g_H/α that the observer measures, with a proportionality constant ℏ/(2πk_B), where ℏ is Planck’s reduced constant and k_B is Boltzmann’s constant. As this thermal radiation climbs out of the horizon’s vicinity and flies off to large radii, its frequencies and temperature get redshifted by the factor α, so as measured by distant observers the temperature is

This suggests a reinterpretation of the first law of black-hole mechanics (26.89) as the first law of thermodynamics for a black hole:

where S_H is the hole’s entropy [cf. Eq. (4.62)]. Show that this entropy is related to the horizon’s surface area by

where

is the Planck length (with G Newton’s gravitation constant and c the speed of light). Because S_H ∝ A_H, the second law of black-hole mechanics (nondecreasing A_H) is actually the second law of thermodynamics (nondecreasing S_H) in disguise.⁶

(h) For a 10-solar-mass, nonspinning black hole, what is the temperature of the Hawking radiation in Kelvins, and what is the hole’s entropy in units of the Boltzmann constant?

(i) Reread the discussions of black-hole thermodynamics and entropy in the expanding universe in Secs. 4.10.2 and 4.10.3, which rely on the results of this exercise.

Transcribed Image Text:

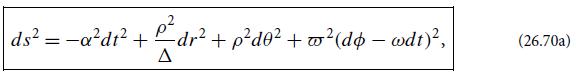
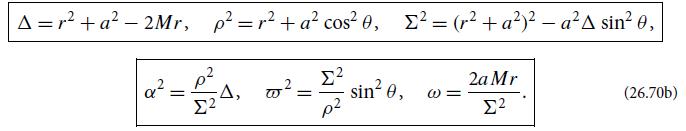
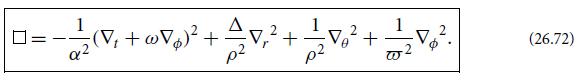
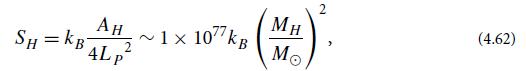
plunge Ex - pplunge.a/at < 0.