A quite different type of accretion disk forms when the gas is unable to cool. This can occur when its gas supply rate is either very large or very small. In the former case, the photons are trapped by the inflowing gas; in the latter, the radiative cooling timescale exceeds the inflow timescale. Either way, pressure and gravity are of comparable importance. There is an elegant description of gas flow close to the black hole as a sort of toroidal star, where the metric is associated with the hole and not the gas. In this problem we make simple assumptions to solve for the equilibrium flow.

(a) Treat the gas as a perfect fluid, and use as thermodynamic variables its pressure P and enthalpy density w. When the gas supply rate is large, the pressure is generally dominated by radiation. Show that in this case w = ρ_o + 4P, with ρ_o the rest mass density of the plasma. Show, further, that w = ρ_o + 5/2P when the pressure is due primarily to nonrelativistic ions and their electrons.

(b) Assume that the motion is purely azimuthal, so the only nonzero covariant components of the gas’s 4-velocity, in the Boyer-Lindquist coordinate system, are u^t and u^∅. Show that the equation of hydrostatic equilibrium (26.31) can be written in the form

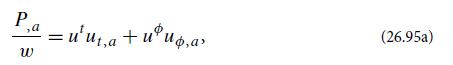
where a = r , θ, and the commas denote partial derivatives.
(c) Define for the gas the specific energy at infinity, ε_∞ = −u_t; the specific fluid angular momentum, ℓ  = −u_∅/u_t; and the angular velocity, Ω = d∅/dt = u∅/u^t. Show that Eq. (26.95a) can be rewritten as

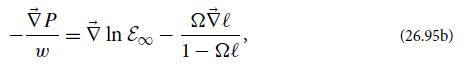
where the spacetime gradient ∇(vector) has components only in the r and θ directions, and ℓ and ε_∞ are regarded as scalar fields.

(d) Now make the first simplifying assumption: the gas obeys a barotropic equation of state, P = P(w). Show that this assumption implies that the specific angular momentum ℓ is a function of the angular velocity.

(e) Show that the nonrelativistic limit of this result—applicable to stars like white dwarfs—is that the angular velocity is constant on cylindrical surfaces, which is von Zeipel’s theorem (Ex. 13.8).

(f) Compute the shape of the surfaces on which Ω and ℓ are constant in the r-θ “plane” (surface of constant t and ∅) for a spinning black hole with a = 0.9M.

(g) Now make the second simplifying assumption: the specific angular momentum ℓ is constant. Compute the shape of the isobars, also in the r-θ plane, and show that they exhibit a cusp along a circle in the equatorial plane, whose radius shrinks as ℓ increases.

(h) Compute the specific energy at infinity, ε_∞, of the isobar that passes through the cusp, and show that it can vanish if ℓ is large enough. Interpret your answer physically.

Equation 26.31.

Data from Exercises 13.8.

Consider a stationary, axisymmetric planet, star, or disk differentially rotating under the action of a gravitational field. In other words, the motion is purely in the azimuthal direction.

(a) Suppose that the fluid has a barotropic equation of state P = P(ρ). Write down the equations of hydrostatic equilibrium, including the centrifugal force, in cylindrical polar coordinates. Hence show that the angular velocity must be constant on surfaces of constant cylindrical radius. This is called von Zeipel’s theorem. (As an application, Jupiter is differentially rotating and therefore might be expected to have similar rotation periods at the same latitudes in the north and the south. This is only roughly true, suggesting that the equation of state is not completely barotropic.)

(b) Now suppose that the structure is such that the surfaces of constant entropy per unit mass and angular momentum per unit mass coincide. (This state of affairs can arise if slow convection is present.) Show that the Bernoulli function (13.51) is also constant on these surfaces.

Transcribed Image Text:

P,a W =u'u₁₁a + uºup,a› (26.95a)