(a) Consider two identical chambers, each with volume V, separated by an impermeable membrane. Into one chamber put energy E and N atoms of helium, and into the other, energy E and N atoms of xenon, with E/N and N/V small enough that the gases are nonrelativistic and nondegenerate. The membrane is ruptured, and the gases mix. Show that this mixing drives the entropy up by an amount △S = 2Nk_B ln 2.

(b) Suppose that energy E and N atoms of helium are put into both chambers (no xenon). Show that, when the membrane is ruptured and the gases mix, there is no increase of entropy. Explain why this result is reasonable, and explain its relationship to entropy being an extensive variable.

(c) Suppose that the N helium atoms were distinguishable instead of indistinguishable. Show this would mean that, in the microcanonical ensemble, they have N! more states available to themselves, and their entropy would be larger by kB ln N! ≈ kB(N ln N − N); and as a result, the Sackur-Tetrode formula (4.42) would be Distinguishable particles:

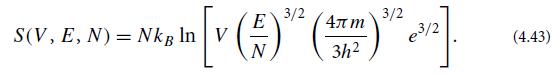
Before the advent of quantum theory, physicists thought that atoms were distinguishable, and up to an additive multiple of N (which they could not compute), they deduced this entropy.

(d) Show that if, as prequantum physicists believed, atoms were distinguishable, then when the membrane between two identical helium-filled chambers is ruptured, there would be an entropy increase identical to that when the membrane between helium and xenon is ruptured: △S = 2Nk_B ln 2 [cf. parts (a) and (b)]. This result, which made prequantum physicists rather uncomfortable, is called the Gibbs paradox.

[v (-)" ()" S(V, E, N) = NkB In V (5)* 3/2 e/2 (4.43)