A good illustration of the importance of the Pv term in the energy flux is provided by the Joule-Kelvin method commonly used to cool gases (Fig. 13.8). Gas is driven from a high-pressure chamber 1 through a nozzle or porous plug into a low-pressure chamber 2, where it expands and cools.

(a) Using the energy flux (13.57), including the Pv term contained in h, show that a mass △M ejected through the nozzle carries a total energy △E₁ that is equal to the enthalpy △H₁ that this mass had while in chamber 1.

(b) This ejected gas expands and crashes into the gas of chamber 2, temporarily going out of statistical (thermodynamic) equilibrium. Explain why, after it has settled down into statistical equilibrium as part of the chamber-2 gas, the total energy it has deposited into chamber 2 is its equilibrium enthalpy △H₂. Thereby conclude that the enthalpy per unit mass is the same in the two chambers, h₁ = h₂.

(c) From h₁ = h₂, show that the temperature drop between the two chambers is

where μ_JK ≡ (∂T /∂P)_h is the Joule-Kelvin coefficient (also called Joule- Thomson). A straightforward thermodynamic calculation yields the identity

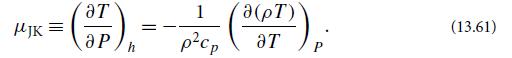
(d) Show that the Joule-Kelvin coefficient of an ideal gas vanishes. Therefore, the cooling must arise because of the attractive forces (van derWaals forces; Sec. 5.3.2) between the molecules, which are absent in an ideal gas. When a real gas expands, work is done against these forces, and the gas therefore cools.

Figure 13.8.

Transcribed Image Text:

P₂ = $₁² P₁ ΔΤ ΔT = MjKd P, (13.60)