(a) Show that the prototypical scalar wave equation (7.17) follows from the variational principle

where L is the lagrangian density

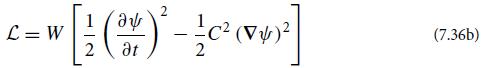
(b) For any scalar-field lagrangian density L(ψ, ∂ψ/∂t , ∇ψ, x, t), the energy density and energy flux can be expressed in terms of the lagrangian, in Cartesian coordinates, as

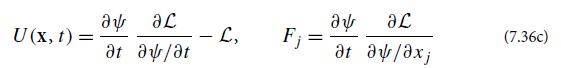
Show, from the Euler-Lagrange equations for L, that these expressions satisfy energy conservation, ∂U/∂t + ∇ . F = 0, if L has no explicit time dependence [e.g., for the lagrangian (7.36b) if C = C(x) and W = W(x) do not depend on time t].

(c) Show that expression (7.36c) for the field’s energy density U and its energy flux F_j agree with Eqs. (7.18).

(d) Now, regard the wave amplitude ψ as a generalized (field) coordinate. Use the lagrangian L = ∫Ld³x to define a field momentum % conjugate to this ψ, and then compute a wave action,

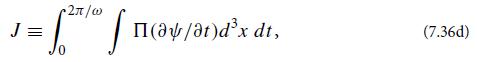
which is the continuum analog of Eq. (7.43) in Sec. 7.3.6. The temporal integral is over one wave period. Show that this J is proportional to the wave energy divided by the frequency and thence to the number of quanta in the wave. It is shown in standard texts on classical mechanics that, for approximately periodic oscillations, the particle action (7.43), with the integral limited to one period of oscillation of q, is an adiabatic invariant. By the extension of that proof to continuum physics, the wave action (7.36d) is also an adiabatic invariant. This means that the wave action and hence the number of quanta in the waves are conserved when the medium [in our case the index of refraction n(x)] changes very slowly in time—a result asserted in the text, and one that also follows from quantum mechanics. We study the particle version (7.43) of this adiabatic invariant in detail when we analyze charged-particle motion in a slowly varying magnetic field in Sec. 20.7.4.

Equations

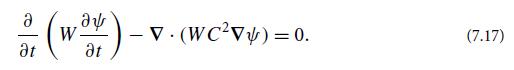
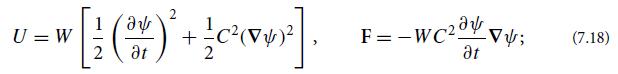
8 ofe Ldtdx = 0, (7.36a)