In this problem, you will calculate the transmission probability through the barrier illustrated in Figure 16.10. We first go through the mathematics leading to the solution. You will then carry out further calculations.

The domain in which the calculation is carried out is divided into three regions for which the potentials are

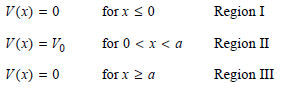
The spatial part of the wave functions must have the following form in the three regions if E < V₀:

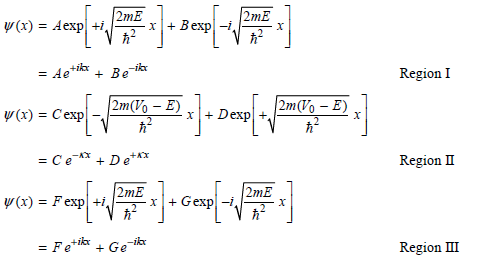
Assume that the wave approaches the barrier from the negative x direction. The coefficient B cannot be set equal to zero because Beˆ’i ˆš2mE/h²)^x represents reflection from the barrier. However, G can be set equal to zero because there is no wave incident on the barrier from the positive x direction.

a. The wave functions and their derivatives must be continuous at x = 0 and x = a. Show that the coefficients must satisfy the following conditions:

b. Because the transmission probability is given by ˆ£F/Aˆ£², it is useful to manipulate these equations to get a relationship between F and A. By adding and subtracting the first pair of equations, A and B can be expressed in terms of C and D. The second pair of equations can be combined in the same way to give equations for D and C in terms of F. Show that

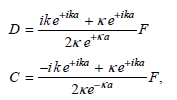
And

c. Substitute these results for C and D in terms of F into

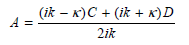
to relate A and F. Show that

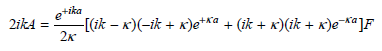
d. Using the hyperbolic trigonometric functions

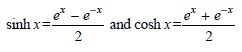
and the relationship cosh²x ˆ’ sinh²x = 1, show that

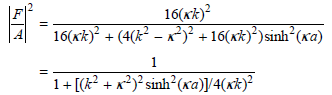
e. Plot the transmission probability for an electron as a function of energy for V₀ = 1.6 Ã— 10^-19J and a = 9.0 × 10^ˆ’10 m up to an energy of 8 × 10^ˆ’19J. At what energy is the tunneling probability 0.1? At what energy is the tunneling probability 0.02?

f. Plot the transmission probability for an electron of energy 0.50 × 10^ˆ’19 J as a function of the barrier width for V₀ = 1.6^-10J between 2 Ã— 10^-10 and 8 × 10^ˆ’10 m. At what barrier width is the transmission probability 0.2?

Transcribed Image Text:

for x <0 V(x) = 0 Region I V(x) = V, V(x) = 0 for 0 < x < a Region II for x 2 a Region III w (x) = Aexp +i, 2mE х| + Вехp| -i, 2mE х = Aetik + Beik Region I y (x) = C'exp 2m(Vo – E) x|+ Dexp |2т (Vo - E) х = Ce A + De*** Region II V (х) %3D Fexp| +і, 2mE x+ Gexp -i, 2mE х = Fetik + Ge Region II