An alternative derivation of the lens equation for a point-mass lens, Eq. (7.88), evaluates the time delay along a path from the source to the observer and finds the true ray by extremizing it with respect to variations of θ.

(a) Show that the geometric time delay is given by

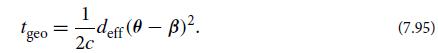
(b) Next show that the lens time delay can be expressed as

where b is the impact parameter. (It will be helpful to evaluate the difference in delays between two rays with differing impact parameters.) This is known as the Shapiro delay.

(c) Show that the lens delay can also be written as

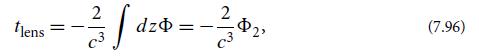
where Ф₂ is the surface gravitational potential obtained by integrating the 3- dimensional potential Φ along the path. The surface potential is only determined up to an unimportant, divergent constant, which is acceptable because we are only interested in dt_lens/db which is finite.(d) By minimizing t_geo + t_lens, derive the lens equation (7.88).

Transcribed Image Text:

geo -deff (0 - 3)². 2c (7.95)