Another interesting 1-dimensional map is provided by the recursion relation

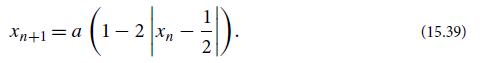
(a) Consider the asymptotic behavior of the variable x_n for different values of the parameter a, with both x_n and a being confined to the interval [0, 1]. In particular, find that for 0 crit (for some a_crit), the sequence x_n converges to a stable fixed point, but for a_critmin, x_max].∼

(b) Using a computer, calculate the value of a_crit and the interval [x_min, x_max] for a = 0.8.

(c) The interval [x_min, x_max] is an example of a strange attractor. It has the property that if we consider sequences with arbitrarily close starting values, their values of x_n in this range will eventually diverge. Show that the attractor is strange by computing the sequences with a = 0.8 and starting values x₁ = 0.5, 0.51, 0.501, and 0.5001.Determine the number of iterations n_∈ required to produce significant divergence as a function of ∈ = x₁− 0.5. It is claimed that n_∈ ∼ln₂(∈). Can you verify this? Note that the onset of chaos at a = a_crit is quite sudden in this case, unlike the behavior exhibited by the Feigenbaum sequence. See Ruelle (1989) for more on strange attractors.

= a (-2 | x - 1/1). 2 Xn+1 = (15.39)