Consider a cell with volume V , like those of Fig. 5.1, that has imaginary walls and is immersed in a bath of identical, nonrelativistic, classical perfect-gas particles with temperature T_b and chemical potential μ_b. Suppose that we make a large number of measurements of the number of particles in the cell and that from those measurements we compute the probability p_N for that cell to contain N particles.

(a) How widely spaced in time must the measurements be to guarantee that the measured probability distribution is the same as that computed, using the methods of this section, from an ensemble of cells (Fig. 5.1) at a specific moment of time?

(b) Assume that the measurements are widely enough separated for this criterion to be satisfied. Show that p_N is given by

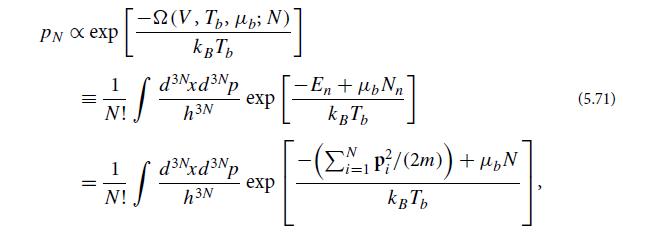
where Ω(V, T_b, μ_b; N) is the grand potential for the ensemble of cells, with each cell constrained to have precisely N particles in it.(c) By evaluating Eq. (5.71) exactly and then computing the normalization constant, show that the probability p_N for the cell to contain N particles is given by the Poisson distribution

where N̅ is the mean number of particles in a cell,

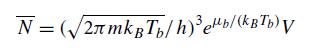
[Eq. (3.39a)].(d) Show that for the Poisson distribution (5.72a), the expectation value is (N) = N̅, and the rms deviation from this is

(e) Show that for 

this Poisson distribution is exceedingly well approximated by a Gaussian with mean N̅ and variance σ_N.

Eq. (3.39a)

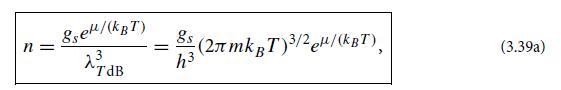
Fig. 5.1

PN o exp N! -&(V, , ; N) d3Nxd3Np h3N I exp[- exp -En + n kBTb d3Nxd3N (Ex=y p?/(2m)) + HN = n exp p -fess> N! h3N kBTb (5.71)