Consider a collection of identical, classical (i.e., with 1) particles with a distribution function N
Question:
Consider a collection of identical, classical (i.e., with η ≪ 1) particles with a distribution function N that is thermalized at a temperature T such that kBT ≪ mc2 (nonrelativistic temperature).(a) Show that the distribution function, expressed in terms of the particles’ momenta or velocities in their mean rest frame, is
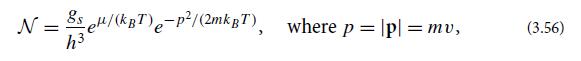
with v being the speed of a particle.
(b) Show that the number density of particles in the mean rest frame is given by Eq. (3.39a).
(c) Show that this gas satisfies the equations of state (3.39b).
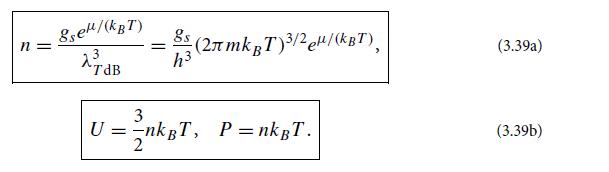
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford
Question Posted:





