Consider a slender flux tube with width much less than its length which, in turn, is much

Question:

Consider a slender flux tube with width much less than its length which, in turn, is much less than the external pressure scale height H. Also assume that the magnetic field is directed along the tube so there is negligible current along the tube.

(a) Show that the requirement of magnetostatic equilibrium implies that inside the flux tube

(b) Consider a segment of this flux tube that is horizontal and has length ℓ. Holding both ends fixed, bend it vertically upward so that the radius of curvature of its center line is R ≫ ℓ. Assume that the fluid is isentropic with adiabatic index γ. By balancing magnetic tension against buoyancy, show that magnetostatic equilibrium is possible if R ≈ 2γH. Do you think this equilibrium could be stable?

(c) In the solar convection zone (cf. Sec. 18.5), small entropy differences are important in driving the convective circulation. Following Ex. 19.20(b), suppose that a length of toroidal field is carried upward by a convecting “blob.” Consider the action of the Coriolis force due to the Sun’s rotation (cf. Sec. 14.2.1) on a single blob, and argue that it will rotate. What will this do to the magnetic field? Sketch the generation of a large-scale poloidal field from a toroidal field through the combined effects of many blobs. What do you expect to observe when a flux tube breaks through the solar surface (known as the photosphere)?

Data from Exercises 19.20.

This problem shows how differential rotation leads to the production of a toroidal magnetic field from a poloidal field.

(a) Verify that for a fluid undergoing differential rotation around a symmetry axis with angular velocity Ω(r, θ), the ∅ component of the induction equation reads

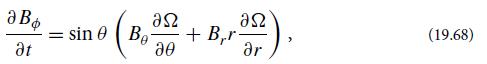
where θ is the co-latitude. (The resistive term can be ignored.)

(b) It is observed that the angular velocity on the solar surface is largest at the equator and decreases monotonically toward the poles. Analysis of solar oscillations (Sec. 16.2.4) has shown that this variation Ω(θ) continues inward through the convection zone (cf. Sec. 18.5). Suppose that the field of the Sun is roughly poloidal. Sketch the appearance of the toroidal field generated by the poloidal field.