Consider a steady, 1-dimensional, large-amplitude electrostatic wave in an unmagnetized, proton-electron plasma. Write down the Vlasov equation for each particle species in a frame moving with the wave [i.e., a frame in which the electrostatic potential is a time-independent function of z, Φ = Φ(z), not necessarily precisely sinusoidal].

(a) Use Jeans’ theorem to argue that proton and electron distribution functions that are just functions of the energy,

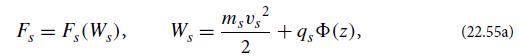
satisfy the Vlasov equation; here s = p, e, and as usual q_p = e, q_e = −e. Then show that Poisson’s equation for the potential Φ can be rewritten in the form

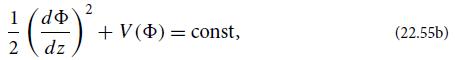
where the potential V is −2/∈₀ times the kinetic-energy density of the particles:

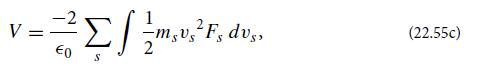
which depends on Φ.

(b) It is possible to find many electrostatic potential profiles Φ(z) and distribution functions F_s[W_s(v, Φ)]that satisfy Eqs. (22.55). These are called BGK waves after Bernstein, Greene, and Kruskal (1957), who first analyzed them. Explain how, in principle, one can solve for (nonunique) BGK distribution functions F_s in a large-amplitude wave of given electrostatic potential profile Φ(z).

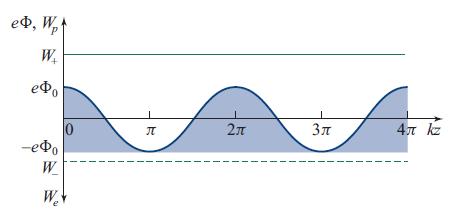
(c) Carry out this procedure, assuming that the potential profile is of the form Φ(z) = Φ₀ cos kz, with Φ₀ > 0. Assume also that the protons are monoenergetic, with W_p = W₊ > eΦ₀, and move along the positive z direction. In addition, assume that there are both monoenergetic (with W_e = W₋ > −eΦ₀), untrapped electrons (also moving along the positive z direction), and trapped electrons with distribution F_e(W_e), −eΦ₀ ≤ W_e 0; see Fig. 22.7. Show that the density of trapped electrons must vanish at the wave troughs [at z = (2n + 1)π/k; n = 0, 1, 2, 3 . . .]. Let the proton density at the troughs be n_p0, and assume that there is no net current. Show that the total electron density can then be written as

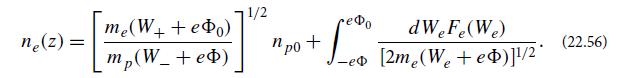
(d) Use Poisson’s equation to show that

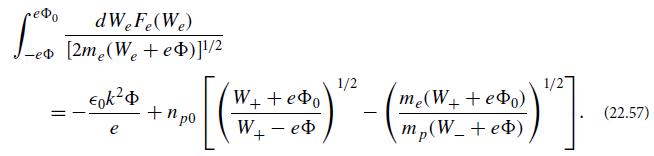
(e) Solve the integral equation in part (d) for F_e(W_e).

(f) Exhibit some solutions of Eq. (22.57) graphically.

Figure 22.57.

F = F,(Ws), W 2 MsVs 2 +9,$(z), (22.55a)