Consider the 1-dimensional flow of shallow water in a straight, narrow channel, neglecting dispersion and boundary layers. The equations governing the flow, a derived and discussed in Box 16.3 and Eqs. (16.23), are

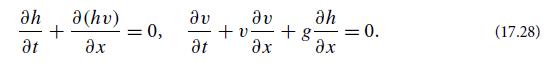
Here h(x, t) is the height of the water, and v(x, t) is its depth-independent velocity.
(a) Find two Riemann invariants J_± for these equations, and find two conservation laws for these J_± that are equivalent to the shallow-water equations (17.28).

(b) Use these Riemann invariants to demonstrate that shallow-water waves steepen in the manner depicted in Fig. 16.4, a manner analogous to the peaking of the nonlinear sound wave in Fig. 17.8.

(c) Use these Riemann invariants to solve for the flow of water h(x, t) and v(x, t) after a dam breaks. The initial conditions (at t = 0) are v = 0 everywhere, and h = h_o at x 0.

Box 16.3.

Equations 16.23.

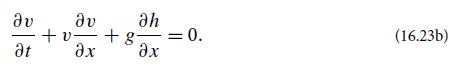
Figure 16.4.

Figure 17.8.

Transcribed Image Text:

Əh + at a(hu) ax = = 0, du at du tu +g ax əh ax = 0. = (17.28)