Consider a black hole or neutron star with mass M at rest in interstellar gas that has constant ratio of specific heats γ. In this exercise you will derive some features of the adiabatic, spherical accretion of the gas onto the hole or star, a problem first solved by Bondi (1952b). This exercise shows how gravity can play a role analogous to a De Laval nozzle: it can trigger a transition of the flow from subsonic to supersonic. Although, near the black hole or neutron star, spacetime is significantly curved and the flow becomes relativistic, we shall confine ourselves to a Newtonian treatment.

(a) Let ρ_∞ and C_∞ be the density and sound speed in the gas far from the hole (at radius r = ∞). Use dimensional analysis to estimate the rate of accretion of mass Ṁ onto the star or hole in terms of the parameters of the system: M, γ , ρ_∞, C_∞, and Newton’s gravitation constant G.

(b) Give a simple physical argument, devoid of dimensional considerations, that produces the same answer for Ṁ , to within a multiplicative factor of order unity, as you deduced in part (a).

(c) Because the neutron star and black hole are both very compact with intense gravity near their surfaces, the inflowing gas is guaranteed to accelerate to supersonic speeds as it falls in. Explain why the speed will remain supersonic in the case of the hole, but must transition through a shock to subsonic flow near the surface of the neutron star. If the star has the same mass M as the hole, will the details of its accretion flow [ρ(r), C(r), v(r)] be the same as or different from those for the hole, outside the star’s shock? Will the mass accretion rates Ṁ be the same or different? Justify your answers physically.

(d) By combining the Euler equation for v(r) with the equation of mass conservation, Ṁ = 4πr²ρv, and with the sound-speed equation C² = (∂P/∂ρ)_s, show that

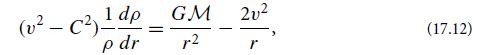
and the flow speed v_s, sound speed C_s, and radius r_s at the sonic point (the transition from subsonic to supersonic; the flow’s critical point) are related by

(e) By combining with the Bernoulli equation (with the effects of gravity included), deduce that the sound speed at the sonic point is related to that at infinity by

and that the radius of the sonic point is

Thence also deduce a precise value for the mass accretion rate Ṁ in terms of the parameters of the problem. Compare with your estimate of Ṁ in parts (a) and (b).

(f) Much of the interstellar medium is hot and ionized, with a density of about 1 proton per cubic centimeter and temperature of about 10⁴ K. In such a medium, what is the mass accretion rate onto a 10-solar-mass hole, and approximately how long does it take for the hole’s mass to double?

Transcribed Image Text:

(v² - c23-dp p dr = GM p2 - 20² r (17.12)