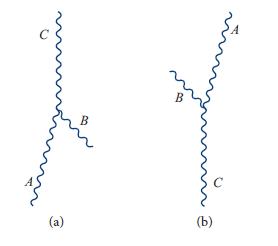
Question: Consider the three-wave processes shown in Fig. 23.5, with A and C Langmuir plasmons and B an ion-acoustic plasmon. The fundamental rate is given by
Consider the three-wave processes shown in Fig. 23.5, with A and C Langmuir plasmons and B an ion-acoustic plasmon. The fundamental rate is given by Eqs. (23.56a) and (23.56b).
(a) By summing the rates of forward and backward reactions (Fig. 23.5a,b), show that the occupation number for the ion-acoustic plasmons satisfies the kinetic equation
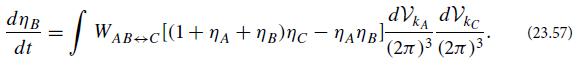
(b) The ion-acoustic plasmons have far lower frequencies than the Langmuir plasmons, so ωB ≪ ωA ≈ ωC. Assume that they also have far lower wave numbers, |kB| ≪ |kA| ≈ |kC|. Assume further (as will typically be the case) that the ionacoustic plasmons, because of their tiny individual energies, have far larger occupation numbers than the Langmuir plasmons, so ηB ≫ ηA ∼ ηC. Using these approximations, show that the evolution law (23.57) for the ion-acoustic waves reduces to the form
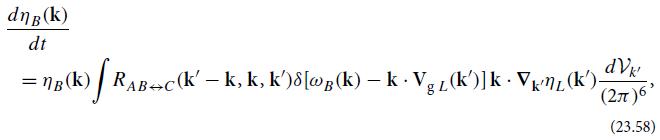
where ηL is the Langmuir (waves A and C) occupation number, Vg L is the Langmuir group velocity, and RC↔BA is the fundamental rate (23.56b).
(c) Notice the strong similarities between the evolution equation (23.58) for the ion-acoustic plasmons that are Cerenkov emitted and absorbed by Langmuir plasmons, and the evolution equation (23.44) for Langmuir plasmons that are Cerenkov emitted and absorbed by fast electrons! Discuss the similarities and the physical reasons for them.
(d) Challenge: Carry out an explicit classical calculation of the nonlinear interaction between Langmuir waves with wave vectors kA and kC to produce ion-acoustic waves with wave vector kB = kC − kA. Base your calculation on the nonlinear Vlasov equation (23.55) and [for use in relating E and f1 in the nonlinear term]the 3-dimensional analog of Eq. (23.13). Assume a spatially independent Maxwellian averaged electron velocity distribution f0 with temperature Te (so ∇f0 = 0). From your result compute, in the random-phase approximation, the evolution of the ion-acoustic energy density εk and thence the evolution of the occupation number η(k). Bring that evolution equation into the functional form (23.58). By comparing quantitatively with Eq. (23.58), read off the fundamental rate RC↔BA. Your result should be the rate in Eq. (23.56b).
Equations:
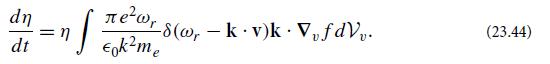

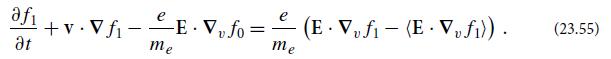
![]()
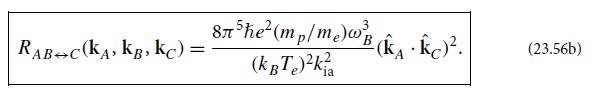
Figure 23.5.
dn B dt = = WAB+c[(1+NA+NB)nc - NAMB dVkA dVkc (2) (2) (23.57)
Step by Step Solution
3.39 Rating (155 Votes )
There are 3 Steps involved in it
To address the questions provided we will follow a stepbystep approach Given the complexity and length of the calculations required I will outline the process and provide a conceptual overview of the ... View full answer

Get step-by-step solutions from verified subject matter experts


