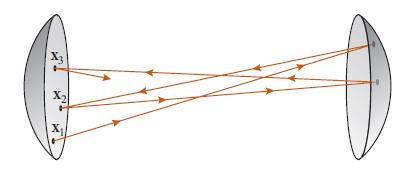
Consider two spherical mirrors, each with radius of curvature R, separated by distance d so as to form an optical cavity (Fig. 7.9). A laser beam bounces back and forth between the two mirrors. The center of the beam travels along a geometric-optics ray.

(a) Show, using matrix methods, that the central ray hits one of the mirrors (either one) at successive locations x₁, x₂, x₃, . . . (where x ≡ (x, y) is a 2-dimensional vector in the plane perpendicular to the optic axis), which satisfy the difference equation

where

Explain why this is a difference-equation analog of the simple-harmonic-oscillator equation.

(b) Show that this difference equation has the general solution

Obviously, A is the transverse position x₀ of the ray at its 0th bounce. The ray’s 0th position x₀ and its 0th direction of motion ẋ₀ together determine B.

(c) Show that if 0 ≤ d ≤ 2R, the mirror system is stable. In other words, all rays oscillate about the optic axis. Similarly, show that if d > 2R, the mirror system is unstable and the rays diverge from the optic axis.

(d) For an appropriate choice of initial conditions x₀ and ẋ₀, the laser beam’s successive spots on the mirror lie on a circle centered on the optic axis. When operated in this manner, the cavity is called a Harriet delay line. How must d/R be chosen so that the spots have an angular step size θ?

Fig 7.9.

Transcribed Image Text:

Xk+2 − 2bXk++X=0, (7.60a)