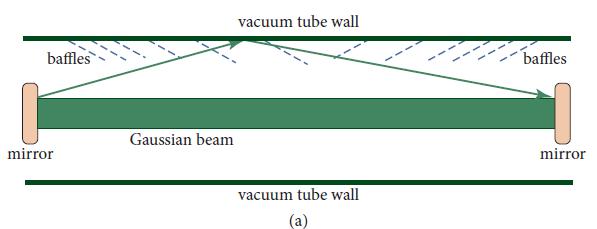
In LIGO and other GW interferometers, one potential source of noise is scattered light. When the Gaussian beam in one of LIGO’s cavities reflects off a mirror, a small portion of the light gets scattered toward the walls of the cavity’s vacuum tube. Some of this scattered light can reflect or scatter off the tube wall and then propagate toward the distant mirror, where it scatters back into the Gaussian beam; see Fig. 8.18a (without the baffles, which are shown dashed). This is troublesome because the tube wall vibrates from sound-wave excitations and seismic excitations, and those vibrations put a phase shift on the scattered light. Although the fraction of all the light that scatters in this way is tiny, the phase shift is huge compared to that produced in the Gaussian beam by gravitational waves. When the tiny amount of scattered light with its huge oscillating phase shift recombines into the Gaussian beam, it produces a net Gaussian-beam phase shift that can be large enough to mask a gravitational wave. This exercise explores some aspects of this scattered-light noise and its control.

(a) The scattering of Gaussian-beam light off the mirror is caused by bumps in the mirror surface (imperfections). Denote by h(x) the height of the mirror surface relative to the desired shape (a segment of a sphere with radius of curvature that matches the Gaussian beam’s wave fronts). Show that, if the Gaussian-beam field emerging from a perfect mirror is ψ^G(x) [Eq. (8.40a)] at the mirror plane, then the beam emerging from the actual mirror is ψ'(x) = ψ^G(x) exp[−i2kh(x)]. The magnitude of the mirror irregularities is very small compared to a wavelength, so |2kh| ≪ 1, and the wave field emerging from the mirror is ψ'(x) = ψ^G(x)[1−i2kh(x)]. Explain why the factor 1 does not contribute at all to the scattered light (where does its light go?), so the scattered light field emerging from the mirror is

(b) Assume that, when arriving at the vacuum-tube wall, the scattered light is in the Fraunhofer region. Then at the tube wall, the scattered light field is given by the Fraunhofer formula

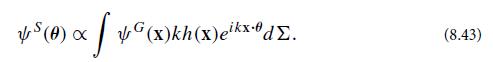
Show that the light that hits the tube wall at an angle θ = |θ| to the optic axis arises from irregularities in the mirror that have spatial wavelengths λ_mirror ∼ λ/θ. The radius of the beam tube is R = 60 cm in LIGO, and the length of the tube (distance between cavity  mirrors) is L = 4 km. What is the spatial wavelength of the mirror irregularities that scatter light to the tube wall at distances z ∼ L/2 (which can then reflect or scatter off the wall toward the distant mirror and there scatter back into the Gaussian beam)? Show that for these irregularities, the tube wall is indeed in the Fraunhofer region.

(c) In the initial LIGO interferometers, the mirrors’ scattered light consisted of two components: one peaked strongly toward small angles so it hit the distant tube wall (e.g., at z ∼ L/2), and the other roughly isotropically distributed. What is the size of the irregularities that produced the isotropic component?

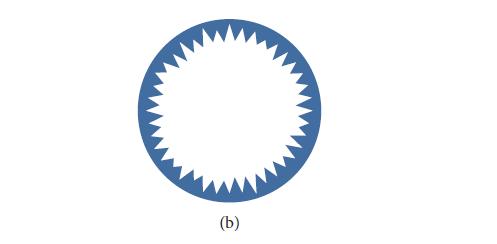
(d) To reduce substantially the amount of scattered light reaching the distant mirror via reflection or scattering from the tube wall, a set of baffles was installed in the tube, in such a way as to hide the wall from scattered light (dashed lines in Fig. 8.18). The baffles have an angle of 35◦ to the tube wall, so when light hits a baffle, it reflects at a steep angle, ∼70◦ toward the opposite tube wall, and after a few bounces gets absorbed. However, a small portion of the scattered light can now diffract off the top of each baffle and then propagate to the distant mirror and scatter back into the main beam. Especially troublesome is the case of a mirror in the center of the beam tube’s cross section, because light that scatters off such a mirror travels nearly the same total distance from the mirror to the top of some baffle and then to the distant mirror, independent of the azimuthal angle φ on the baffle at which it diffracts. There is then a danger of coherent superposition of all scattered light that diffracts off all angular locations around any given baffle—and coherent superposition means a much enlarged net noise. To protect against any such coherence, the baffles in the LIGO beam tubes are serrated (i.e., they have sawtooth edges), and the heights of the teeth are drawn from a random (Gaussian) probability distribution (Fig. 8.18b). The typical tooth heights are large enough to extend through about six Fresnel zones. How wide is each Fresnel zone at the baffle location, and correspondingly, how high must be the typical baffle tooth? By approximately how much do the random serrations reduce the light-scattering noise, relative to what it would be with no serrations and with coherent scattering?

(e) To aid you in answering part d, show that the propagator (point-spread function) for light that begins at the center of one mirror, travels to the edge of a baffle, and then propagates to the center of the distant mirror is

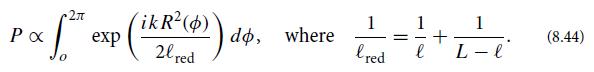
Here R(∅) is the radial distance of the baffle edge from the beam tube axis at azimuthal angle ∅ around the beam tube, and at distance ℓ down the tube from the scattering mirror. Note that ℓ_red is the “reduced baffle distance” analogous to the reduced mass in a binary system. One can show that the time-varying part of the scattered-light amplitude (i.e., the part whose time dependence is produced by baffle vibrations) is proportional to this propagator. Explain why this is plausible. Then explain how the baffle serrations, embodied in the ∅ dependence of R(∅), produce the reduction of scattered-light amplitude in the manner described in part c.

Figure 8.18 a and b

Transcribed Image Text:

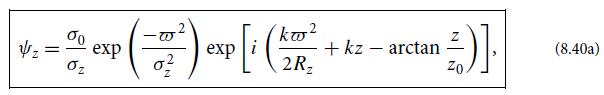
y(x) = -iy (x)2kh (x). (8.42)