Derive Eq. (11.55) relating the angle o = (d/dx) x = 0 = k o =
Question:
Derive Eq. (11.55) relating the angle θo = (dη/dx)x = 0 = kηo = πηo/ℓ to the applied force F when the card has an n = 1, arched shape.
(a) Derive the first integral of the elastica equation
![]()
where θo is an integration constant. Show that the boundary condition of no bending torque (no inflection of the card’s shape) at the card ends implies θ = θo at x = 0 and x = ℓ; whence θ = 0 at the card’s center, x = ℓ/2.
(b) Integrate the differential equation (11.59) to obtain
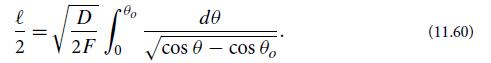
(c) Perform the change of variable sin(θ/2) = sin(θo/2) sin ∅ and thereby bring Eq. (11.60) into the form
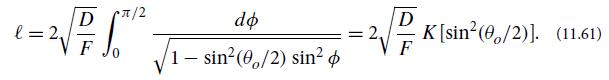
Here K(y) is the complete elliptic integral of the first type, with the parameterization used by Mathematica (which differs from that of many books).
(d) Expand Eq. (11.61) in powers of θo/2 to obtain
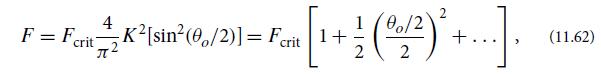
from which deduce our desired result, Eq. (11.55).
Eq. (11.55)
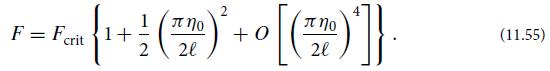
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





