Consider a slender wire of rectangular cross section with horizontal thickness h and vertical thickness w that is resting on a horizontal surface, so gravity is unimportant. Let the wire be bent in the horizontal plane as a result of equal and opposite forces F that act at its ends; Fig. 11.10. The various shapes the wire can assume are called elastica; they were first computed by Euler elastica in 1744 and are discussed in Love (1927, pp. 401–404). The differential equation that governs the wire’s shape is similar to that for the cantilever [Eq. (11.45)], with the simplification that the wire’s weight does not enter the problem and the complication that the wire is long enough to deform through large angles.

It is convenient (as in the cantilever problem, Fig. 11.8) to introduce curvilinear coordinates with coordinate x measuring distance along the neutral surface, z measuring distance orthogonal to x in the plane of the bend (horizontal plane), and y measured perpendicular to the bending plane (vertically). The unit vectors along the x, y, and z directions are e_x, e_y, e_z (Fig. 11.10). Let θ(x) be the angle between e_x and the applied force F; θ(x) is determined, of course, by force and torque balance.

(a) Show that force balance along the x and z directions implies

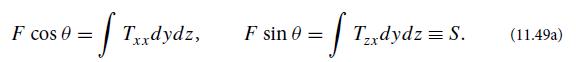
(b) Show that torque balance for a short segment of wire implies

where M(x) ≡  ∫zT_xxdydz is the bending torque.

(c) Show that the stress-strain relation in the wire implies

where D = Ewh³/12 is the flexural rigidity [Eq. (11.41b)].

(d) From the relations in parts (a)–(c), derive the following differential equation for the shape of the wire:

This is the same equation as describes the motion of a simple pendulum!

(e) For Track-Two readers who have studied Sec. 11.8: Go back through your analysis and identify any place that connection coefficients would enter into amore careful computation, and explain why the connection-coefficient terms are negligible.

(f) Find one nontrivial solution of the elastica equation (11.49d) either analytically using elliptic integrals or numerically. (The general solution can be expressed in terms of elliptic integrals.)

(g) Solve analytically or numerically for the shape adopted by the wire corresponding to your solution in part (f), in terms of precisely Cartesian coordinates (X, Z) in the bending (horizontal) plane. Express the curvature of the wire, 1/R = dθ/dx, as

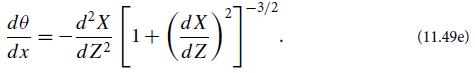
(h) Obtain a uniform piece of wire and adjust the force F to compare your answer with experiment.

Equation 11.45

Figure 11.8.

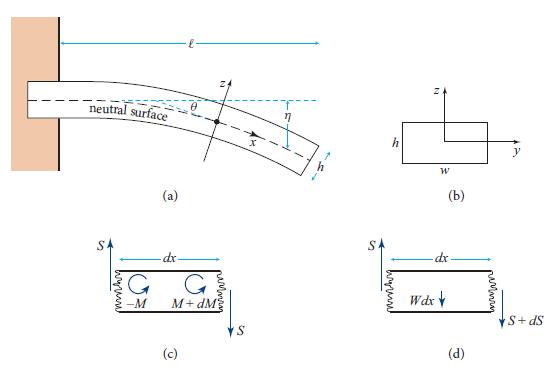
Fig.11.10.

Transcribed Image Text:

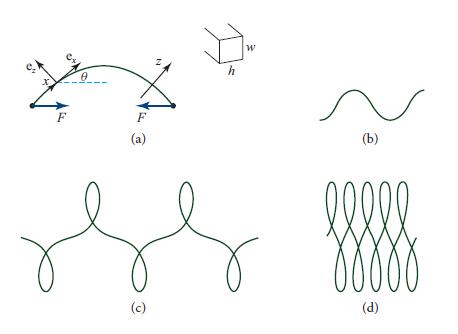
F cos 0 = [ Txxdydz, S F sin 0 = = [ Tzxdydz = S. (11.49a)