Fill in the details of the analysis of time-averaged seeing in Box 9.2.More specifically, do the following.
Question:
Fill in the details of the analysis of time-averaged seeing in Box 9.2.More specifically, do the following. If you have difficulty, Roddier (1981) may be helpful.
(a) Give an order-of-magnitude derivation of Eq. (4a) in Box 9.2 for the mean-square phase fluctuation of light induced by propagation through a thin, turbulent layer of atmosphere.
(b) Deduce the factor 2.91 in Eq. (4a) in Box 9.2 by evaluating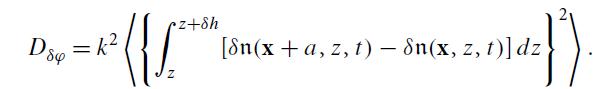
(c) Derive Eq. (4b) in Box 9.2 for the time-averaged complex visibility after propagating through the thin layer.
(d) Use the point-spread function (8.28) for free propagation of the light field ψ to show that, under free propagation, the complex visibility γ⊥(a, z, t) = (ψ(x + a, z, t)ψ∗(x, z, t)) (with averaging over x and t) is constant (i.e., independent of height z).
(e) By combining parts c and d, deduce Eqs. (5) in Box 9.2 for the mean-square phase fluctuations and spacetime-averaged visibility on the ground.
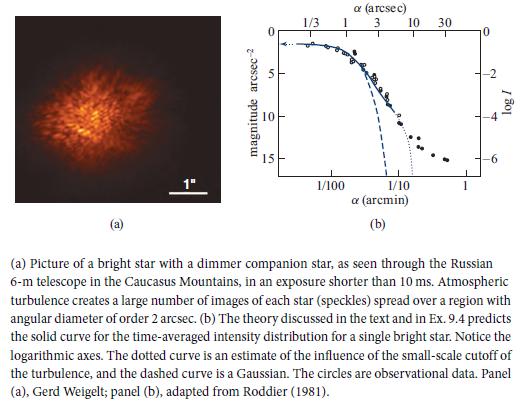
(f) Perform a numerical Fourier transform of γ̅⊥(a) [Eq. (5b) in Box 9.2] to get the time-averaged intensity distribution I (α). Construct a log-log plot of it, and compare with panel b of the first figure in Box 9.2.What is ro for the observational data shown in that figure?
(g) Re-express the turbulence-broadened image’s FWHM as
![]()
Show that the Airy intensity distribution for light for a circular aperture of diameter D [Eq. (8.18)] has
![]()
(h) The fact that the coefficients in these two expressions for αFWHM are both close to unity implies that when the diameter
![]()
the seeing is determined by the telescope. Conversely, when
![]()
(which is true for essentially all ground-based research optical telescopes), it is the atmosphere that determines the image quality. Large telescopes act only as “light buckets,” unless some additional correctives are applied, such as speckle image processing or adaptive optics (Box 9.2).A common measure of the performance of a telescope with or without this correction is the Strehl ratio, S, which is the ratio of the peak intensity in the actual image of a point source on the telescope’s optic axis to the peak intensity in the Airy disk for the telescope’s aperture. Show that without correction, S = 1.00(ro/D)2.Modern adaptive optics systems on large telescopes can achieve S ∼ 0.5.
Eq. 8.18.
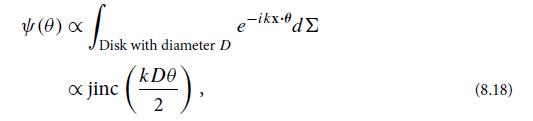
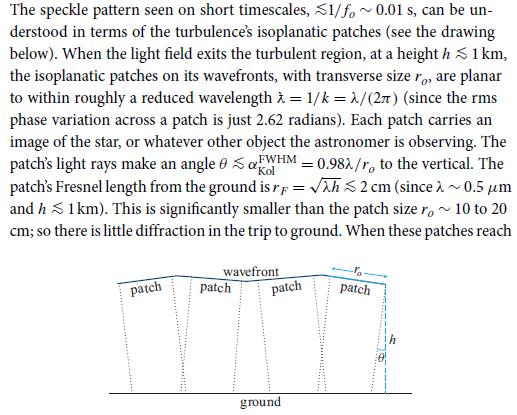
Box 9.2.










Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford




