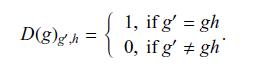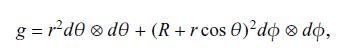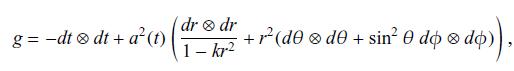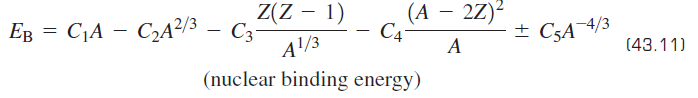University Physics with Modern Physics 13th edition Hugh D. Young, Roger A. Freedman, A. Lewis Ford - Solutions

Discover comprehensive solutions for "University Physics with Modern Physics 13th edition" by Hugh D. Young, Roger A. Freedman, and A. Lewis Ford. Access an extensive collection of answers key, solutions manual, and solutions pdf to enhance your understanding. Dive into solved problems, chapter solutions, and step-by-step answers tailored to each question. Perfect for students, instructors, and self-learners, our resources include a complete test bank and instructor manual. Explore this invaluable textbook's questions and answers, all available for free download. Elevate your learning experience with our expertly crafted solutions!