Let the metric on a two-dimensional torus $T^{2}$ with radii $r$ and $R>r$ be $$begin{equation*} g=r^{2} d
Question:
Let the metric on a two-dimensional torus $T^{2}$ with radii $r$ and $R>r$ be
$$\begin{equation*}
g=r^{2} d \theta \otimes d \theta+(R+r \cos \theta)^{2} d \phi \otimes d \phi \tag{5.398}
\end{equation*}$$
where $\theta$ and $\phi$ take values in the interval [0,2 $\pi$ ). Find the geodesic equation(s) on a torus with the metric (5.398), by doing the following.
(i) Using the variational principle and the action of a free massive point particle. As a first step, substitute the torus metric into the appropriate Lagrangian.
(ii) Calculating the Christoffel symbols and substituting them into the general geodesic equation.
Which method do you expect to be easier? Next, do the following.
(iii) Solve the equations. Are there conserved quantities?
(iv) Sketch some examples of geodesics on a torus.
Data from 5.398
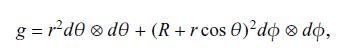
Step by Step Answer:

Mathematical Methods For Physics An Introduction To Group Theory Topology And Geometry
ISBN: 9781107191136
1st Edition
Authors: Esko Keski Vakkuri, Claus Montonen, Marco Panero




