Spatially homogeneous and isotropic universe. The Robertson-Walker metric $$begin{equation*} g=-d t otimes d t+a^{2}(t)left(frac{d r otimes d
Question:
Spatially homogeneous and isotropic universe. The Robertson-Walker metric
$$\begin{equation*}
g=-d t \otimes d t+a^{2}(t)\left(\frac{d r \otimes d r}{1-k r^{2}}+r^{2}\left(d \theta \otimes d \theta+\sin ^{2} \theta d \phi \otimes d \phi\right)\right) \tag{5.399}
\end{equation*}$$
where $k$ can be $-1,0$, or 1 , describes a spatially homogenous and isotropic spacetime. Calculate the Riemann tensor, the Ricci tensor, and the scalar curvature associated with the metric (5.399).
Data from 5.399
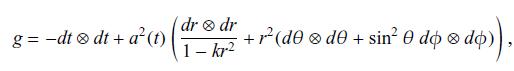
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Mathematical Methods For Physics An Introduction To Group Theory Topology And Geometry
ISBN: 9781107191136
1st Edition
Authors: Esko Keski Vakkuri, Claus Montonen, Marco Panero
Question Posted:





