For a soap film that is attached to a bent wire (e.g., to the circular wire that
Question:
For a soap film that is attached to a bent wire (e.g., to the circular wire that a child uses to blow a bubble), the air pressure on the film’s two sides is the same. Therefore, Eq. (16.16) (with γ replaced by 2γ , since the film has two faces) tells us that at every point in the film, its two principal radii of curvature must be equal and opposite:R1 = −R2. It is an interesting exercise in differential geometry to show that this requirement means that the soap film’s surface area is an extremum with respect to variations of the film’s shape, holding its boundary on the wire fixed. If you know enough differential geometry, prove this extremal-area property of soap films, and then show that for the film’s shape to be stable, its extremal area must actually be a minimum.
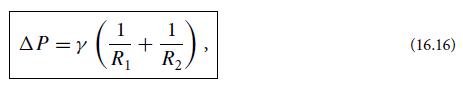
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





