Highly stable clocks (e.g., cesium clocks, hydrogen maser clocks, or quartz crystal oscillators) have angular frequencies

Question:

Highly stable clocks (e.g., cesium clocks, hydrogen maser clocks, or quartz crystal oscillators) have angular frequencies ω of ticking that tend to wander so much over very long timescales that their variances diverge. For example, a cesium clock has random-walk noise on very long timescales (low frequencies)

and correspondingly,

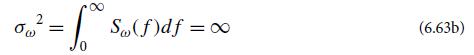
For this reason, clockmakers have introduced a special technique for quantifying the frequency fluctuations of their clocks. Using the phase

they define the quantity

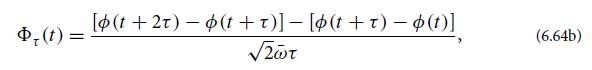
where ω̅ is the mean frequency. Aside from the √2, this Ф_τ(t) is the fractional difference of clock readings for two successive intervals of duration τ . (In practice the measurement of t is made by a clock more accurate than the one being studied; or, if a more accurate clock is not available, by a clock or ensemble of clocks of the same type as is being studied.)

(a) Show that the spectral density of τ (t) is related to that of ω(t) by

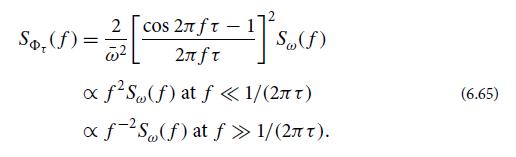
(b) The Allan variance of the clock is defined as

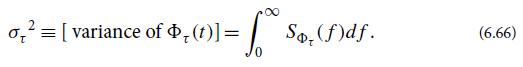
Show that

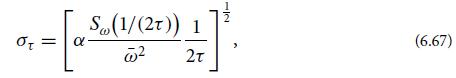
where α is a constant of order unity that depends on the spectral shape of S_ω(f) near f = 1/(2τ). Explain why, aside from the factor α, the right-hand side of Eq. (6.67) is the rms fractional fluctuation of ω at frequency 1/(2τ) in bandwidth 1/(2τ).

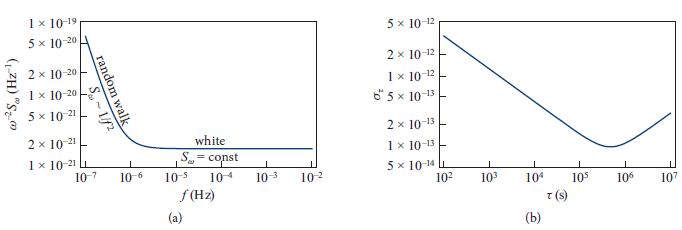
(c) Show that, if ω has a white-noise spectrum, then the clock stability is better for long averaging times than for short; if ω has a flicker-noise spectrum, then the clock stability is independent of averaging time; and if ω has a random-walk spectrum, then the clock stability is better for short averaging times than for long. (See Fig. 6.11.)

Fig. 6.11