In Ex. 3.17, we studied the diffusion of particles through an infinite 3-dimensional medium. By solving the
Question:
In Ex. 3.17, we studied the diffusion of particles through an infinite 3-dimensional medium. By solving the diffusion equation, we found that, if the particles’ number density at time t = 0 was no(x), then at time t it has become
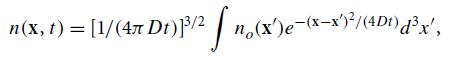
where D is the diffusion coefficient [Eq. (3.73)].
(a) For any one of the diffusing particles, the location y(t) in the y direction (one of three Cartesian directions) is a 1-dimensional random process. From the above n(x, t), infer that the conditional probability distribution for y is

(b) Verify that the conditional probability (6.13) satisfies the Smoluchowski equation (6.11).
At first this may seem surprising, since a particle’s position y is not Markov. However, the diffusion equation from which we derived this P2 treats as negligibly small the timescale τr on which the velocity dy/dt thermalizes. It thereby wipes out all information about what the particle’s actual velocity is, making y effectively Markov, and forcing its P2 to satisfy the Smoluchowski equation.
Equation (6.11).
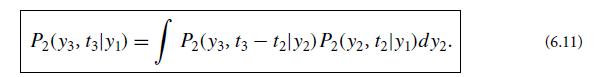
Data from Exercises 3.17
Show that the following is a solution to the diffusion equation (3.71) for particles in a homogeneous infinite medium:

![]()
and that it satisfies ∫ndVx = N, so N is the total number of particles. Note that this is a Gaussian distribution with width σ = √4Dt. Plot this solution for several values of σ. In the limit as t → 0, the particles are all localized at the origin. As time passes, they random-walk (diffuse) away from the origin, traveling a mean distance ασ = α√4Dt after time t, where α is a coefficient of order one. We will meet this square-root-of-time evolution in other random-walk situations elsewhere in this book.
Suppose that the particles have an arbitrary initial distribution no(x) at time t = 0. Show that their distribution at a later time t is given by the following Green’s function integral:
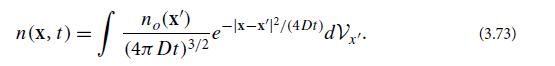
What form does the solution take in one dimension? And in two dimensions?
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford




