Our study of the Schwarzschild solution of Einsteins equations in this chapter has been confined to situations
Question:
Our study of the Schwarzschild solution of Einstein’s equations in this chapter has been confined to situations where, at small radii, the Schwarzschild geometry joins onto that of a star—either a static star or one that implodes to form a black hole. Suppose, by contrast, that there is no matter anywhere in the Schwarzschild spacetime. To get insight into this situation, construct an embedding diagram for the equatorial 2-surfaces {t = const, θ = π/2} of the vacuum Schwarzschild spacetime, using as the starting point the line element of such a 2-surface written in isotropic coordinates (Ex. 26.3):
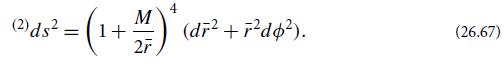
Show that the region 0
Data from Exercises 26.3.
(a) It turns out that the following line element is a solution of the vacuum Einstein field equation G = 0:
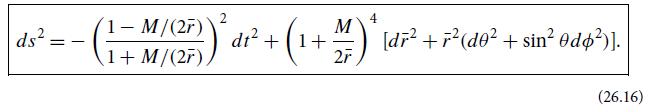
Since this solution is spherically symmetric, Birkhoff’s theorem guarantees it must represent the standard Schwarzschild spacetime geometry in a coordinate system that differs from Schwarzschild’s. Show that this is so by exhibiting a coordinate transformation that converts this line element into Eq. (26.1).
(b) Show that at large radii r ≫ M, the line element (26.16) takes the form (25.98c) discussed in Chap. 25, but with vanishing spin angular momentum J = 0.
Equations.
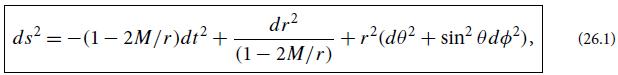
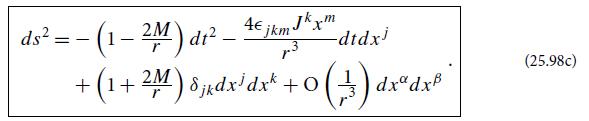
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





