The cosmic dawn that preceded the epoch of reionization can be probed by low frequency CMB observations using a special radio hyperfine line emitted and absorbed by hydrogen atoms. This line is associated with a flip in direction of the magnetic dipole associated with the central proton relative to the magnetic field created by the orbiting electron. The line’s frequency and strength can be calculated using quantum mechanics. For our purposes, all that we need to know is that the frequency associated with the transition is ν_H = 1.42GHz, the degeneracy of the ground/upper state is 1/3, and the rate of spontaneous transition is A = 3× 10⁻¹⁵ s⁻¹ (Ex. 28.9).

(a) Explain why these hyperfine transitions should produce a change in the measured CMB spectrum over a range of frequencies∼20–150 MHz, where the lower limit is due to the practicality of making the measurement.

(b) Consider hydrogen atoms with total number density n₁ in the ground state and n₂ = 3n₁ exp(−hν_H/k_BT_S) in the excited state, where T_S defines the spin temperature, and we measure frequencies and rates locally. Show that the net creation rate of photons per unit volume and frequency can be written as 3n₁Aδ(ν − ν_H)(1− T_γ/T_S).

(c) Hence, show that the CMB temperature fluctuation at frequency ν₀ = ν_H/a, produced when the expansion factor was a, is

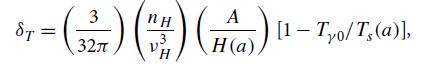
where n_H is the atomic hydrogen density, H(a) is the expansion rate, and T_γ0 is the CMB temperature today while T_γ is the CMB temperature at the point of emission.

(d) It is predicted that T_S ∼ 10 K when a ∼ 0.05. Estimate the associated temperature perturbation, δ_T.

The spin temperature T_s will follow the nonrelativistic gas and fall faster than the radiation temperature T_γ , creating absorption above ∼10 MHz. The first stars will heat the gas and create Lyman alpha photons, which end up populating the upper hyperfine state, increasing the spin temperature and reducing the absorption above ∼50 MHz. Black holes are expected to create highly penetrating X-rays, which may make T_s > T_γ and lead to emission above 100 MHz. Eventually the gas will be fully ionized, so that the spectrum above ∼200 MHz should be unaffected.

At the lowest frequencies observable today, the radiation from our galaxy is ∼300 times brighter than the CM Band has to be carefully removed, along with the influence of the ionosphere. Most attention is now(2016) focused on measuring a signal associated with the growing density perturbations from the time just before reionization. If the measurements are successful, we will have another powerful probe of the growth of matter perturbations.

Data from Exercises 28.9.

In our discussion of recombination, we related the emission of Lyman α photons to their absorption. This involves some important ideas in the theories of radiation and thermodynamics.

(a) Consider a population of two-state atoms. Let the number of atoms in the lower state be N₁ and in the upper state N₂. The probability per unit time of an upperstate atom changing to a lower state and releasing a photon of energy hν equal to the energy difference of the states is denoted by A. We expect that the rate of upward, 1→2 transitions is proportional to the occupation number η_γ of the photons with frequency ν. Call this rate K_uη_γ. By requiring that the atoms should be able to remain in Boltzmann equilibrium with the Planckian radiation field of the same temperature, show that there must also be downward, stimulated emission at a rate per state-2 atom of Kdηγ , and show that K_u = K_d = A.

(b) The absorption cross section σ for an atom at rest can be written in the Lorentz or Breit-Wigner form as:

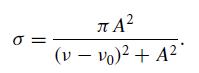
Either make a classical model of an atom as an electron oscillator with natural frequency ν₀, or use time-dependent perturbation theory in quantum mechanics to justify the form of this formula.
(c) Identify the frequency probability function P_ν introduced in Sec. 28.4.4, and plot the natural line profile for an emission line.

(d) Atoms also have thermal motions, which Doppler shift the photon frequencies. Modify the line profile by numerically convolving the natural profile with a 1- dimensional Gaussian velocity distribution and replot it, drawing attention to its behavior when A is much more than the thermal Doppler shift.

(e) We have restricted our attention to a two-state system. It is usually the case that we are dealing with energy levels containing several distinct states, and the formalism we have described has to be modified to include the degeneracies g_i of these levels. Make the necessary corrections and recover the formulas used in the text.

(f) A second complication is polarization. Discuss how to include this.

Transcribed Image Text:

3 A ST -=(2+) (") (то) и [1 - To/T (a)], 3 32л H(a) H