Consider a small satellite in a noncircular orbit about a spherical body with much larger mass M, for which the external gravitational field is Schwarzschild. The satellite will follow a timelike geodesic. Orient the Schwarzschild coordinates so the satellite’s orbit is in the equatorial plane: θ = π/2.

(a) Because the metric coefficients are independent of t and ∅, the satellite’s energy at- infinity ε_∞ = −p_t and angular momentum L = p_∅ must be constants of the satellite’s motion (Ex. 25.4a). Show that

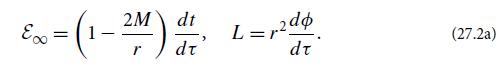
Here and below we take the satellite to have unit mass, so its momentum and 4-velocity are the same, and its affine parameter ζ and proper time τ are the same.

(b) Introduce the coordinate u = r⁻¹ and use the normalization of the 4-velocity to derive the following differential equation for the orbit:

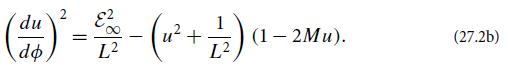
(c) Differentiate this equation with respect to ∅ to obtain a second-order differential equation:

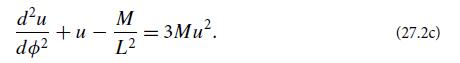
By reinstating the constants G, c, and comparing with the Newtonian orbital equation, argue that the right-hand side represents a relativistic perturbation to the Newtonian equation of motion.

(d) Henceforth in this exercise, assume that r ≫ M (i.e., u ≪ 1/M), and solve the orbital equation (27.2c) by perturbation theory. More specifically, at zero order (i.e., setting the right-hand side to zero), show that the Kepler ellipse

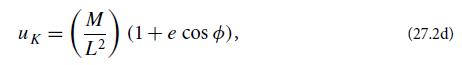
is a solution. Here e (a constant of integration) is the ellipse’s eccentricity, and L²/M is the ellipse’s semi-latus rectum, p. The orbit has its minimum radius at ∅ = 0.

(e) By substituting u_K from part (d) into the right-hand side of the relativistic equation of motion (27.2c), show (to first-order in the relativistic perturbation) that in one orbit the angle ∅ at which the satellite is closest to the mass advances by △∅ ≈ 6πM²/L².

(f) For the planet Mercury, using the parameter values given after Eq. (27.1), deduce  that the relativistic contribution to the rate of advance of the perihelion (point of closest approach to the Sun) is 42.98" per century.

Equations 27.1.

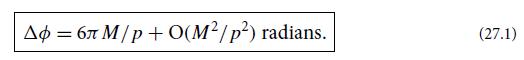
Data from Exercises 25.4a.

(a) Suppose that in some coordinate system the metric coefficients are independent of some specific coordinate x^A: g_αβ,A = 0 (e.g., in spherical polar coordinates {t , r , θ , ∅} in flat spacetime g_αβ,∅ = 0, so we could set x^A = ∅). Show that

is a constant of the motion for a freely moving particle [p_∅ = (conserved z component of angular momentum)in the above, spherically symmetric example].

Note the analogy of the constant of the motion p_A with Hamiltonian mechanics: there, if the hamiltonian is independent of x^A, then the generalized momentum p_A is conserved; here, if the metric coefficients are independent of x^A, then the covariant component p_A of the momentum is conserved. For an elucidation of the connection between these two conservation laws

Ex = (1-2M) d dt dr L=p2dd dr (27.2a)