Consider the light propagating outward from the beam splitter, along the x arm of an interferometric gravitational-wave detector, as analyzed in TT gauge, so (suppressing the subscript “x arm” and superscript “out”) the electromagnetic vector potential is

with A^α constant and with

(a) Show that this φ satisfies the nullness equation (27.84), as claimed in the text—which implies that A^α = R(A^αe^{iφ(x, t)}) satisfies Maxwell’s equations in the geometric-optics limit.

(b) Show that this φ satisfies the initial condition (27.85), as claimed in the text.

(c) Show that, because the gradient k(vector) = ∇(vector)φ of this φ satisfies k(vector) · k(vector) = 0, it also satisfies

Thus, the wave vector is the tangent vector to geometric-optics rays that are null geodesics in the gravitational-wave metric. Photons travel along these null geodesics and have 4-momenta p(vector) = ℏk(vector).

(d) Because the gravitational-wave metric (27.80) is independent of x, the p_x component of a photon’s 4-momentum must be conserved along its geodesic world line. Compute p_x = k_x = ∂φ/∂x, and thereby verify this conservation law.

(e) Explain why the photon’s frequency, as measured by observers at rest in our TT coordinate system, is ω = −k_t = −∂φ/∂t . Explain why the rate of change of this frequency, as computed moving with the photon, is dω/dt ≈ (∂/∂t + ∂/∂x)ω, and show that dω/dt ≈ −1/2ω_odh/dt.

Equations.

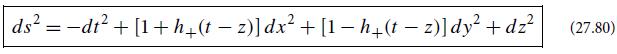
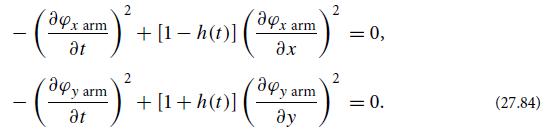
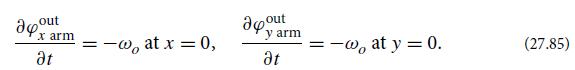
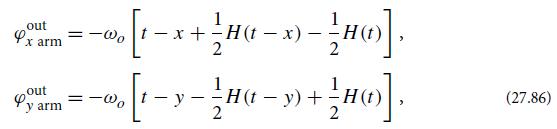
A = R(Aeig(x,1)),