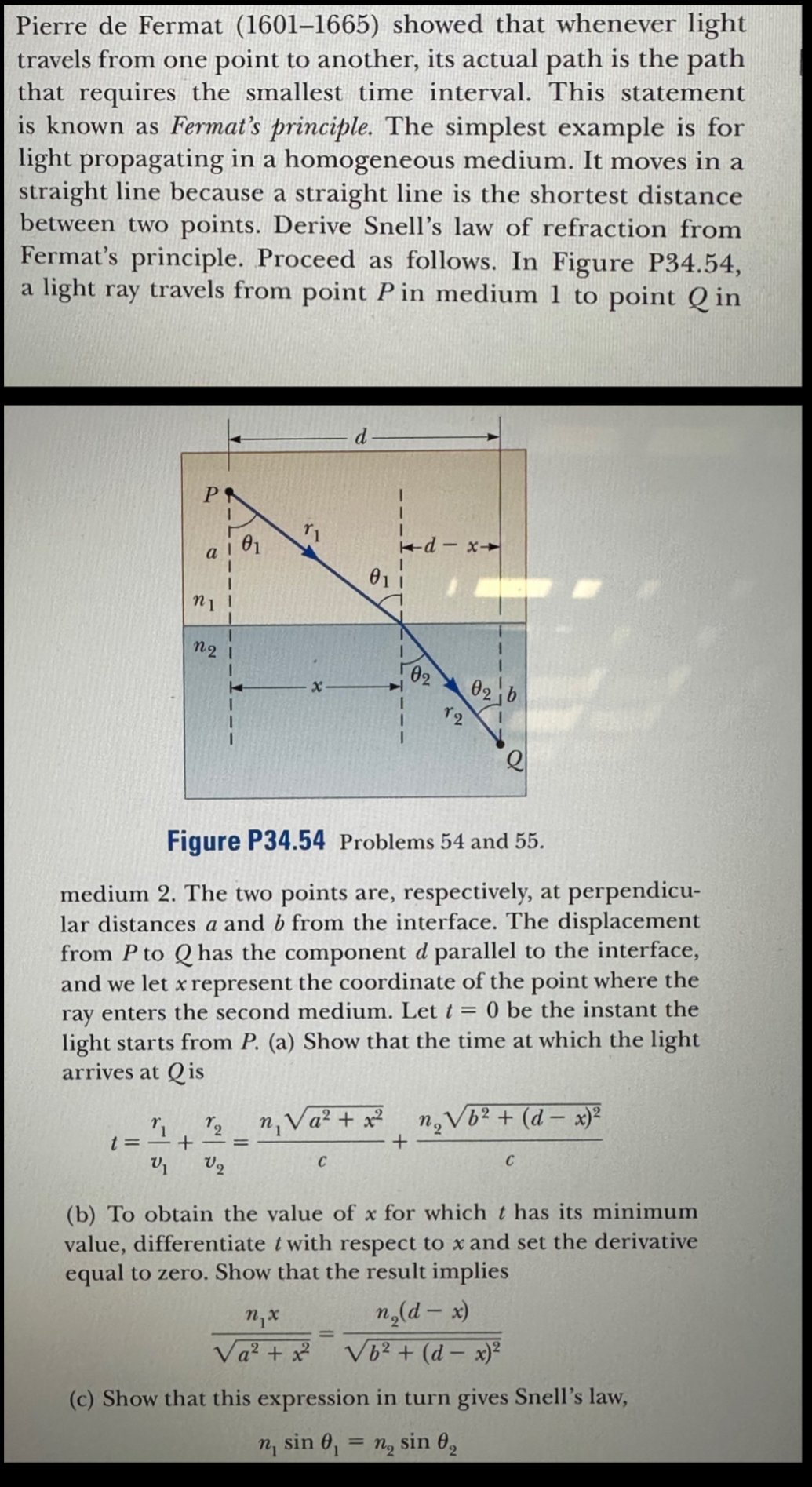
Pierre de Fermat (1601-1665) showed that whenever light travels from one point to another, its actual path is the path that requires the smallest time interval. This statement is known as Fermat's principle. The simplest example is for light propagating in a homogeneous medium. It moves in a straight line because a straight line is the shortest distance between two points. Derive Snell's law of refraction from Fermat's principle. Proceed as follows. In Figure P34.54, a light ray travels from point P in medium 1 to point Q in d P a I 01 01 d-x- n21 02 02 b X 12 I e Figure P34.54 Problems 54 and 55. medium 2. The two points are, respectively, at perpendicu- lar distances a and b from the interface. The displacement from P to Q has the component d parallel to the interface, and we let x represent the coordinate of the point where the ray enters the second medium. Let t = 0 be the instant the light starts from P. (a) Show that the time at which the light arrives at Qis t= + 12 n Va + x2 nb + (d- x)2 = + V2 C C (b) To obtain the value of x for which t has its minimum value, differentiate t with respect to x and set the derivative equal to zero. Show that the result implies nx = n(d- x) Va + b + (d- x)2 (c) Show that this expression in turn gives Snell's law, n, sin 0 = n2 sin 02