The form of the potential energy functional derived in the text [Eq. (19.47)] is optimal for demonstrating
Question:
The form of the potential energy functional derived in the text [Eq. (19.47)] is optimal for demonstrating that the operator F̂ is self-adjoint. However, there are several simpler, equivalent forms that are more convenient for practical use.
(a) Use Eq. (19.46) to show that

where b ≡ δB is the Eulerian perturbation of the magnetic field.
(b) Insert Eq. (19.58) into expression (19.56b) for the potential energy W[ξ] and convert the volume integral of the divergence into a surface integral. Then impose the boundary condition of a vanishing normal component of the magnetic field at ∂V [Eq. (19.20b)] to show that

(c) Consider axisymmetric perturbations of the cylindrical Z-pinch of an incompressible fluid, as discussed in Sec. 19.5.2, and argue that the surface integral vanishes.
(d) Adopt a simple trial eigenfunction, and obtain a variational estimate of the growth rate of the sausage instability’s fastest growing mode.
Equations.
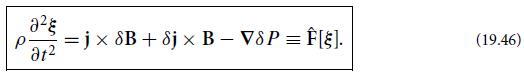

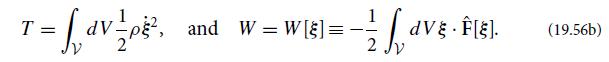
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





