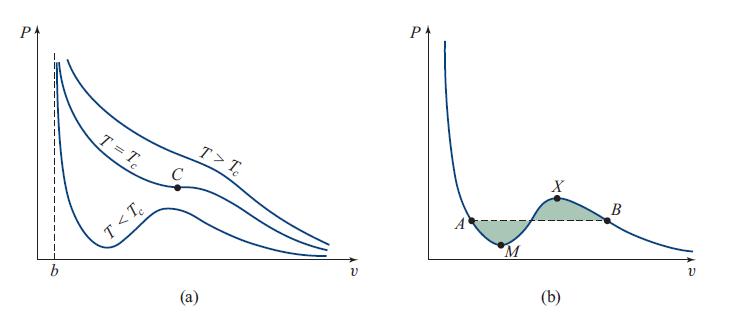
The van der Waals equation of state (P + a/v²)(v − b) = k_BT for H₂O relates the pressure P and specific volume (volume per molecule) v to the temperature T ; see Sec. 5.7. Figure 5.8 makes it clear that, at some temperatures T and pressures P, there are three allowed volumes v(T , P), one describing liquid water, one water vapor, and the third an unstable phase that cannot exist in Nature. At other values of T and P, there is only one allowed v. The transition between three allowed v values and one occurs along some curve in the T -P plane—a catastrophe curve.

(a) This curve must correspond to one of the elementary catastrophes explored in the previous exercise. Based on the number of solutions for v(T , P), which catastrophe must it be?

(b) Change variables in the van der Waals equation of state to p = P/P_c− 1, τ = T/T_c − 1, and ρ = v_c/v − 1, where T_c = 8a/(27bk_B), Pc = a/(27b²), and vc = 3b are the temperature, pressure, and specific volume at the critical point C of Fig. 5.8. Show that this change of variables brings the van derWaals equation of state into the form

where z = −(p/3 + 8τ/3) and x = 2p/3 − 8τ/3.(c) This equation ρ³ − zρ − x is the equilibrium surface associated with the catastrophe-theory potential

Correspondingly, the catastrophe [the boundary between three solutions v(T , P) and one] has the universal cusp form x =±2(z/3)^2/3 [Eq. (7.75)]. Plot this curve in the temperature-pressure plane.

Fig. 5.8

Transcribed Image Text:

p³ - zp - x = 0, 3 (7.83)