We will study classical sound waves propagating through an isotropic, elastic solid. As we shall see, there
Question:
We will study classical sound waves propagating through an isotropic, elastic solid. As we shall see, there are two types of sound waves: longitudinal with frequency-independent speed CL, and transverse with a somewhat smaller frequency independent speed CT . For each type of wave, s = L or T , the material of the solid undergoes an elastic displacement
![]()
where A is the wave amplitude, fs is a unit vector (polarization vector) pointing in the direction of the displacement, k is the wave vector, and ω is the wave frequency. The wave speed is Cs = ω/|k| (= CL or CT). Associated with these waves are quanta called phonons. As for any wave, each phonon has a momentum related to its wave vector by p = ℏk, and an energy related to its frequency by E = ℏω. Combining these relations we learn that the relationship between a phonon’s energy and the magnitude p = |p| of its momentum is E = Csp. This is the same relationship as for photons, but with the speed of light replaced by the speed of sound! For longitudinal waves fL is in the propagation direction k, so there is just one polarization, gL = 1. For transverse waves fT is orthogonal to k, so there are two orthogonal polarizations (e.g., fT = ex and fT = ey when k points in the ez direction), gT = 2.
(a) Phonons of both types, longitudinal and transverse, are bosons. Why?
(b) Phonons are fairly easily created, absorbed, scattered, and thermalized. A general argument that we will give for chemical reactions in Sec. 5.5 can be applied to phonon creation and absorption to deduce that, once they reach complete thermal equilibrium with their environment, the phonons will have vanishing chemical potential μ = 0.What, then, will be their distribution functions η and N?
(c) Ignoring the fact that the sound waves’ wavelengths λ = 2π/|k| cannot be smaller than about twice the spacing between the atoms of the solid, show that the total phonon energy (wave energy) in a volume V of the solid is identical to that for blackbody photons in a volume V , but with the speed of light c replaced by the speed of sound Cs, and with the photon number of spin states, 2, replaced by gs = 3 (2 for transverse waves plus 1 for longitudinal): Etot = asT4V, with ![]()
[cf. Eqs. (3.54)].
(d) Show that the specific heat of the phonon gas (the sound waves) is CV = 4asT3V . This scales as T3, whereas in a metal the specific heat of the degenerate electrons scales as T (previous exercise), so at sufficiently low temperatures the electron specific heat will dominate over that of the phonons.
(e) Show that in the phonon gas, only phonon modes with wavelengths longer than ∼ λT = Csh/(kBT) are excited; that is, for λ ≪ λT the mean occupation number is η ≪ 1; for λ ∼ λT , η ∼ 1; and for λ >> λT, η >> 1. As T is increased, λT gets reduced. Ultimately it becomes of order the interatomic spacing, and our computation fails, because most of the modes that our calculation assumes are thermalized actually don’t exist. What is the critical temperature (Debye temperature) at which our computation fails and the T3 law for CV changes? Show by a roughly one-line argument that above the Debye temperature, CV is independent of temperature.
Equation 3.54.
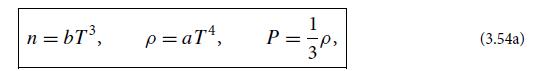
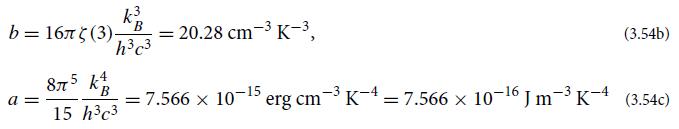
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





