We have described distribution functions for particles and photons and the forms that they have in thermodynamic
Question:
We have described distribution functions for particles and photons and the forms that they have in thermodynamic equilibrium. An extension of these principles can be used to constrain the manner in which particles and photons interact, specifically, to relate the emission and absorption of radiation.
(a) Consider a two-level (two-state) electron system with energy separation E = hν0. Suppose that an electron can transition with a probability per unit time, A, from the upper level (u) to the lower level (l), creating a photon in a specific state. Use the Boltzmann distribution, ignoring degeneracy, Eq. (3.22d), and the expression for the mean photon occupation number, Eq. (3.23), to show that, when the electrons and photons are in thermal equilibrium at the same temperature T , then:
![]()
where nl ,u are the number densities of the electrons in the two states, and ηγ is the photon mean occupation number.
(b) The three terms in Eq. (3.26) are often called the rates per unit volume for spontaneous emission, stimulated emission, and (stimulated) absorption, respectively. (The second and third terms are sometimes expressed using Einstein B coefficients.) The expressions Anu, Anuηγ , and An∫ηγ for the rates of these three types of transition are commonly (and usually correctly) assumed to apply out of thermodynamic equilibrium as well as in equilibrium. Discuss briefly two conditions that need to be satisfied for this to be so: that all three types of transition proceed in a manner that is independent of anything else present, and that the stimulated transitions are time reversible. What additional condition needs to be satisfied if the electron system is more complex than a two-level system?
(c) Typical transitions have some duration τ, which implies that the photons will be emitted with a distribution of frequencies with width △ν ∼ τ−1 about ν0. They may also not be emitted isotropically and can carry polarization. Denote the state of a photon by its frequency ν, direction of travel ![]()
and polarization i = 1 or 2,

(d) Further generalize the results in part c by assuming that, instead of occupying just two states, the electrons have a continuous distribution of momenta and radiate throughout this distribution. Express the classical emissivity and absorption coefficient as integrals over electron momentum space.
(e) Finally, consider the weak nuclear transformation ν + n → e + p, where the neutron n and the proton p can be considered as stationary. Explain carefully why the rate at which this transformation occurs can be expressed as
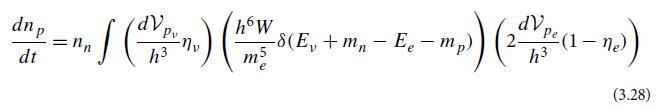
for some W. It turns out that W is a constant (Weinberg, 2008). What is the corresponding rate for the inverse reaction?
Data from Equation 3.22(d) and 3.23 equation

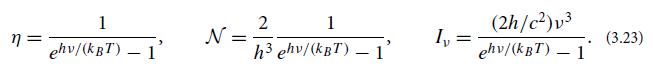
Step by Step Answer:

Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics
ISBN: 9780691159027
1st Edition
Authors: Kip S. Thorne, Roger D. Blandford





