Figure P2.21 shows two pendulums suspended from frictionless pivots and connected at their midpoints by a spring . Assume that each pendulum can be represented by a mass M at the end of a massless bar of length L. Also assume that the displacement is small and linear approximations can be used for sinθ and cos θ. The spring located in the middle of the bars is unstretched when . θ₁ = θ₂ The input force is represented by f(t), which influences the left-hand bar only.

(a) Obtain the equations of motion, and sketch a block diagram for them.

(b) Determine the transfer function T(s) = θ? (s)/F (s). 

(c) Sketch the location
of the poles and zeros of T(s) on the s-plane.

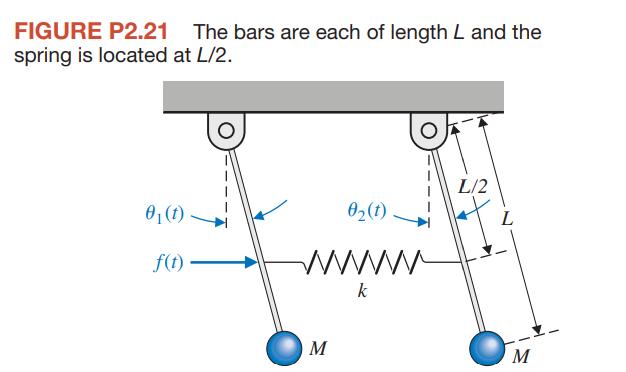
FIGURE P2.21 The bars are each of length L and the spring is located at L/2. 0 (1) f(t) 0 (t) wwww k M L/2 L M