(a) Derive the generalizedwave equation satisfied by E(r, t) in non magnetic matter when the permittivity is a function of position, (r). Specialize the equation to the case when (r) = (z) and E(r, t) = ˆxE(z, t ).
(b) Let E(z, t) = E(z) exp(−iωt) and let (z) = ε₀[1 + α cos(2k₀z)]. Show that the Fourier components Ê(k) of the electric field satisfy the coupled set of linear equations

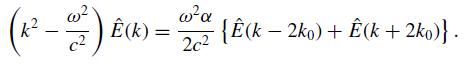
(c) Suppose α 0, i.e., k = k₀ + q where |q|0.
Show that the Fourier components Ê(q + k₀) and Ê(q − k₀) are larger than all others and, therefore, that a 2 × 2 eigenvalue problem determines the dispersion relation. Hint: The wave frequency cannot differ greatly from its α = 0 value in the limit considered.
(d) Solve the eigenvalue problem to find ω(k₀, q). Study its behavior analytically at q = 0. Sketch the complete dispersion curve and show that there is a range of frequencies—called a photonic band gap—where no waves occur.

(4 2/) () = 2/ 1 k (k) {(k-2ko) + E(k+2ko)}.