A set of particles has charges qk , masses mk , and positions rk(t ). Let be the space-time four-vector and define . The components of the stress-energy tensor for this system are the sum of the density and current density of energy-momentum of the individual particles:

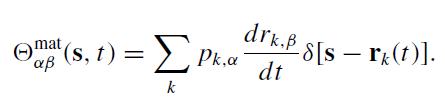
(a) Prove that Θ^mat αβ = Θ ^mat _βα.
(b) Prove that ∂_β Θ^mat_αβ = j_νF_αν . This divergence is the negative of the divergence of the electromagnetic stress-energy tensor. Therefore, ∇ · (Θ + Θ^mat) = 0. Begin with the space divergence ∂_iΘ_αi ^mat.

Transcribed Image Text:

3=(x, y, z, ict)