(a) Show that the frequency of any mode (E,B) of a resonant cavity with volume V can...
Question:
(a) Show that the frequency of any mode (E,B) of a resonant cavity with volume V can be computed from
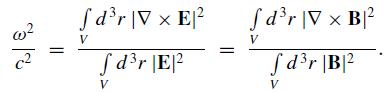
(b) Suppose E → E + δE or B → B + δB, where δE and δB satisfy the boundary conditions. Prove that the change in ω2 is only second-order in δE or δB. This implies that any choice of E(r) or B(r) in these formulae which satisfies the boundary conditions (but not the Maxwell equations) provides an upper bound on the lowest mode frequency.
(c) Obtain an estimate of the lowest TM-mode frequency in a cylindrical cavity of radius R by minimizing the frequency with respect to the variational parameter a in the choice B = (ρ + aρ2)ϕ̂ . Compare your answer with the exact result.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
b Suppose E E or B B where E and B satisfy the boundary conditions Prove that the change in u2 i...View the full answer
Answered By
NEETA SINGH
I’m not going to lie, I haven’t always wanted to be in education. It wasn’t until I was a sophomore in high school that I realized that education was something I was interested in. It all started when I really started falling in love with my volunteer work at a camp that works with people living with disabilities. My experiences at that camp influenced me to want to major in severe special education.
Though my path towards education started early on in my high school years, my first official teaching experience was not until this past summer. I got to work as a kindergarten teacher at a summer school at my church, and it was one of the best experiences of my life. I have always loved children, especially kindergarten through second grade children, so I was very excited about my position.
Of course, I was incredibly nervous on my first day of teaching. First of all, I wasn’t even sure if I was cut out to be a teacher, and second of all, the thought of watching and teaching a bunch of rowdy five year olds was overwhelming, to say the least. Nonetheless, my first day in the classroom went better than I expected. My job as their teacher was to teach them the alphabet, how to spell words, and simple math, like counting. Though the learning content was not difficult, coming up with six weeks worth of lesson plans was something that I had never done before. At first, it was incredibly difficult for me to figure out what I should do for every day, but with time, the process got a little bit easier, and I started getting more creative with the lessons.
My first teaching experience taught me a lot about what it means to be a teacher and a lot about myself, as a future educator. For example, I always knew that coming up with lesson plans was not easy, so I’m glad that I was able to have this experience to prepare me for it in the future. I also learned that I do not have a good sense of time when I am teaching, so I now know to make sure to make a schedule of what will be done at what time.
0 Reviews
10+ Question Solved
Related Book For 
Question Posted:
