In the absence of free charge or free current, the Maxwell equations in optically active matter are

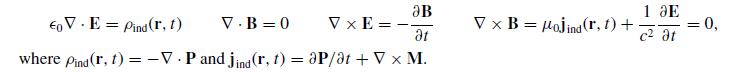
(a) Let P = (ϵ − 0)E and M = (μ − 1 0 − μ −1)B, but do not introduce D or H. Assume plane wave behavior for all relevant quantities, e.g., E(r, t) = E(k, ω) exp[i(k · r − ωt)]. Find j_ind(k, ω) and ρind(k, ω). Explain why your expression for ρ_ind(k, ω) is the most general scalar that can be constructed from k, E, and B that is linear in the fields. Explain why your expression for j_ind(k, ω) is not the most general vector than can be constructed from the same ingredients. 

(b) Let ξ be a real constitutive constant. Explain why a term ξ added to jωBind in part (a) produces a completely general current density vector and show that ϵωE + μ ⁻¹k × B + iξωB = 0.
(c) Show that the propagating waves in the medium of part (b) are determined by an equation of the form

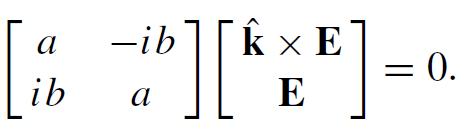
(d) Show that the solutions in part (c) are right and left circularly polarized waves that obey different dispersion relations. Find the range of allowed values of ξ . Matter that behaves this way is called optically active.
(e) Show that the constitutive relations D = E + βB and B = μH + γE give an equivalent description of optical activity. How are the two constants β and γ related to ξ?

Transcribed Image Text:

ƏB €0V. E = Pind (r, t) VxE= at where Pind(r, t) = -V.P and jind (r, t) = aP/ât + V x M. V.B=0 == V x B= Moj ind(r, t) +. 1 JE c² at = 0,