Roll up an ohmic sheet to form an infinitely long, origin-centered cylinder of radius a. Cut a narrow slot along the length of the cylinder and insert a line source of EMF so the electrostatic potential within the sheet (in polar coordinates) is

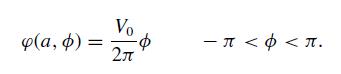
(a) Find a separated-variable solution to Laplace’s equation in polar coordinates for the electrostatic potential inside and outside the cylinder.(b) Sum the series in part (a) and show that the equipotentials inside the cylinder are straight lines drawn from the seat of the EMF.

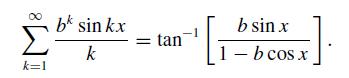
(c) Prove that the potential outside the cylinder is dipolar and indicate the direction of the dipole moment. Sketch several equipotentials inside and outside the cylinder.(d) Show that the surface charge density on both sides of the cylinder wall is σ(α) = (ε₀V₀/2πa) tan α, where α is a polar angle defined with respect to the seat of the EMF.(e) Show that the electric field inside the cylinder is E = −(V₀/πs)ˆα, where s is the polar distance from the seat of the EMF. Sketch several electric field lines inside and outside the cylinder. Take some care with the angle at which the field lines approach the cylinder.

(,) = = Vo -