The annulus shown below is cut from a planar metal sheet with thickness t and conductivity σ.

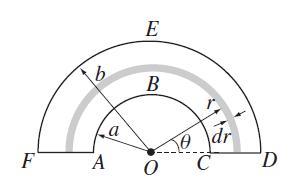
(a) Let V be the voltage between the edge CD and the edge FA. Solve Laplace’s equation to find the electrostatic potential, current density, and resistance of the annulus.
(b) Divide the annulus into a sequence of concentric sub-annuli, each with width dr. Show how to combine the resistances of the individual sub-annuli to reproduce the resistance computed in part (a). Use the lines of current density predicted in each case to explain why the two calculations agree.
(c) Let V be the voltage between the edge ABC and the edge DEF of the original annulus. Repeat all the steps of part (a) and part (b).
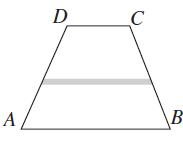
(d) The trapezoid shown below is cut from a planar metal sheet with thickness t and conductivity σ. Let V be the voltage between the edge AB and the edge CD. by solving Laplace’s equation for the entire trapezoid is not the same as the resistance computed by summing the resistances for sub-trapezoids like the one indicated by shading in the figure below. Does the summation calculation overestimate or underestimate the exact resistance?

Transcribed Image Text:

F b A a E B O 50 dr C D