The optical properties of a remarkable class of materials called topological insulators (TI) are captured by constitutive
Question:
The optical properties of a remarkable class of materials called topological insulators (TI) are captured by constitutive relations which involve the fine structure constant, α = (e2/ − hc) / (4π ϵ0). With α0 = α √ ϵ0/μ0, the relations are
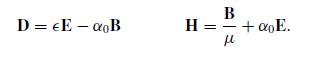
(a) Begin with the Maxwell equations in matter with no free charge or current. Show that a monochromatic plane wave of (E,B) is a solution of these equations for a TI and find the wave speed.
(b) A plane wave with linear polarization impinges at normal incidence on the flat surface of a TI. Show that the transmitted wave remains linearly polarized with its electric field rotated by an angle θF. This is called Faraday rotation of the plane of polarization.
(c) Show that the reflected wave remains linearly polarized with its electric field rotated by an angle θK. This is called Kerr rotation of the plane of polarization.
Step by Step Answer:
a b c For a plane wave varying as expikr wt the Ma...View the full answer
