This problem outlines a contour integration method to prove that See Problem 8.23 for another method. (a)
Question:
This problem outlines a contour integration method to prove that
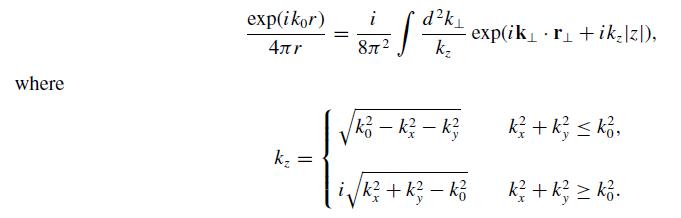
See Problem 8.23 for another method.
(a) The left side of the Weyl identity is the free-space Green function, G0(r), which satisfies (∇2 + k20)G0(r) = −δ(r). Fourier transform this differential equation and show that
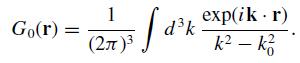
(b) Use contour integration to perform the integral over kz in part (a). Assume that k0 has a small positive imaginary part to establish the location of the poles and to decide how to close the contour.
Data From Problem 8.23
Write δ(r − r') = δ(r⊥ − r'⊥)δ(z − z') and use direct integration to derive Weyl’s formula for the free-space Green function in three dimensions,
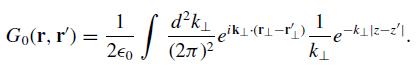
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





