A cantilever beam bends under a uniform load w per unit length and is subject to an axial force P at its free end. For small deflections a numerical approximation to the shape of the beam is given by the set of equations

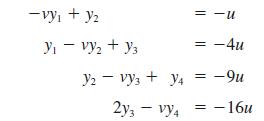
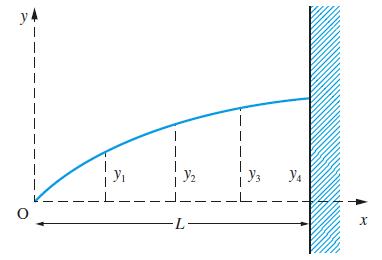
The deflections are indicated on Figure 5.7. The parameter v is defined as

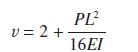
where EI is the flexural rigidity and L is the length of the beam. The parameter u = wL⁴/32EI. Use either Cramer’s rule or the adjoint matrix to solve the equations when v = 3 and u = 1. Note the immense effort required to solve this very simple problem using these methods. In later sections much more efficient methods will be described. A computer package such as MATLAB should be used to check the results.

Figure 5.7