A uniform horizontal beam OA, of length a and weight w per unit length, is clamped horizontally at O and freely supported at A. The transverse displacement y of the beam is governed by the differential equation

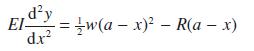
where x is the distance along the beam measured from O, R is the reaction at A, and E and I are physical constants. At O the boundary conditions are

Solve the differential equation. What is the boundary condition at A? Use this boundary condition to determine the reaction R. Hence find the maximum transverse displacement of the beam.

Transcribed Image Text:

El- =w(a - x) - R(a - x) ,dy d.x